Деление двузначных, трехзначных и многозначных чисел столбиком

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

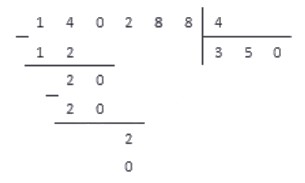
3. Выполняем операцию вычитания  и под чертой записываем результат.

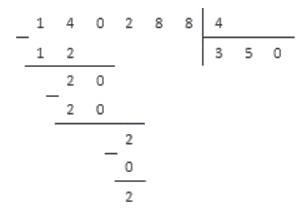
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

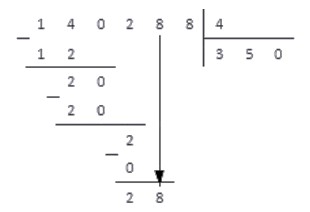
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

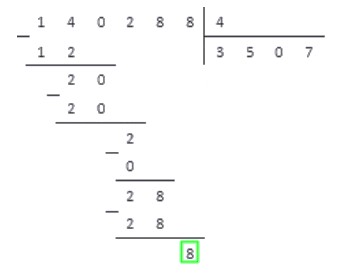
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

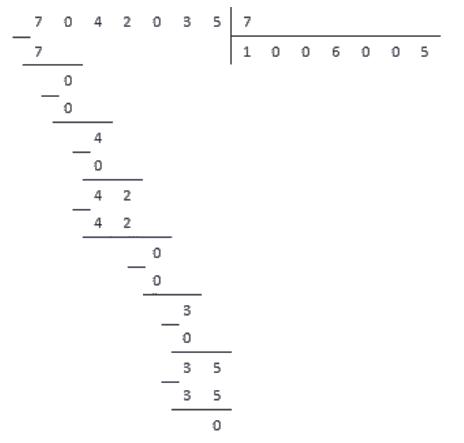
Ответ: 1006005

Деление с остатком на 10, 100, 1 000

Рассмотрите внимательно примеры . На какие две группы можно их разделить?

79 : 10          450 : 10           900 : 100          817 : 100    95 000 : 1 000         95 600 : 1 000

Запишем в первый столбик примеры на деление без остатка, а во второй – с остатком.

450 : 10     900 : 100     95 000 : 1 000

79 : 10    817 : 100   95 600 : 1 000

Вспомним, как разделить число на 10, 100, 1 000. При делении на 10  у делимого убираем один нуль, при делении на 100 – убираем два нуля, при делении на 1 000 – убираем три нуля. Очень просто! Решим примеры первого столбика.

450 : 10 = 45    

 900 : 100 = 9    

95 000 : 1 000 = 95 

А какое правило действует при делении на 10, 100, 1 000 с остатком?

У делимого не будем убирать цифры, а только лишь отступим (с конца) на одну цифру, если делим на 10, на две – если делим на 100, на три – если делим на 1 000. Вот так:

79 : 10           79

817 : 100          817

95 600 : 1 000       95 600

Получаем ответ и остаток.

79 : 10 = 7 (ост. 9)

817 : 100 = 8 (ост. 17)

95 600 : 1 000 = 95 (ост. 600)

Сделаем проверку умножением и прибавим остаток.

7 ∙ 10 + 9 = 79

8 ∙100 + 17 = 817

95 ∙ 1 000 + 600 = 95 600

Решили верно.

Ребята, помните о том, что при делении остаток должен быть меньше делителя!

Давайте проверим это правило в наших примерах.

79 : 10 = 7 (ост. 9)  9< 10

817 : 100 = 8 (ост. 17)  17 <100

95 600 : 1 000 = 95 (ост. 600)  600 < 1 000

Следующие примеры решите самостоятельно. Обязательно сравните остаток с делителем. Выполните проверку умножением.

714 : 100

54 : 10

78 340 : 1 000

Проверь себя.

714 : 100 = 7 (ост.14)  14 < 100    7 ∙ 100 + 14 = 714

54 : 10 = 5 (ост.4)  4 < 10    5 ∙ 10 + 4 = 54

78 340 : 1 000 = 78 (ост.340)  340 < 1 000    78 ∙ 1 000 + 340 = 78 340

Умножение суммы на число

Задание. Посчитайте и запишите решение на вопрос: сколько квадратов в прямоугольнике?

Вариант 1. Рассуждайте так: в ряду шесть синих квадратов плюс три красных квадрата. Рядов 4. Значит, запишите решение:

Сумма в скобках равна девяти. 9 ∙ 4 = 36. Это табличное умножение.

Вариант 2. Количество квадратов подсчитайте другим способом. Узнайте, сколько синих, потом, сколько красных, полученные результаты сложите.

Таким способом удобно умножать большие величины.

Любое двузначное число легко записать как сумму разрядных слагаемых: круглых десятков и единиц.

Умножайте сначала десятки, потом единицы, произведения складывайте.

Как это сделать, рассмотрите на примере.

Сумму десяти и пяти умножим на шесть.

Это распределительное свойство умножения суммы на число.

Правило умножения суммы на число запишите буквенным выражением.

За внимание награждаю вас оранжевой лентой. Идите по маршруту дальше

Идите по маршруту дальше.

Связь деления с умножением

Чтобы проследить связь между делением и умножением, вспомним, что деление представляется, как разбиение исходного делимого множества на несколько одинаковых множеств. Умножение связано с объединением нескольких одинаковых множеств в одно. 

Деление — действие, обратное умножению. Что это значит? Приведем аналогию. Представим, что у нас есть b множеств, в каждом из которых — по с предметов. Общее количество предметов во всех множествах равно a. Умножение — это объединение всех множеств в одно. Математически оно запишется так:

b·c=a.

Обратный процесс разбиения полученного общего множества на b множеств по с предметов в каждом соответствует делению:

a÷b=c.

На основе сказанного можно перейти к следующему утверждению:

Если произведение натуральных чисел c и b равно a, то частное чисел a и b равно c. Перепишем в буквенном виде. 

Если b·c=a, то a÷b=c

Пользуясь переместительным свойством умножения, можно записать:

c·b=a

Отсюда также следует, что a÷с=b. 

На основании сказанного можно сформулировать общий вывод. Если произведение чисел c и b равно a, то соответственно частные a÷b и a÷c равны c и b.

Подытожим все изложенное выше и дадим определение деления натуральных чисел.

Деление натуральных чисел

Деление — нахождение неизвестного множителя по известному произведению и другому известному множителю.

Это определение станет базой, на основе которой мы будем строить правила и методы деления натуральных чисел.

Правило встречается в следующих упражнениях:

2 класс

Страница 67. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 74,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 11. Вариант 2. № 1,
Моро, Волкова, Проверочные работы

Страница 29. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 40. Вариант 1. № 6,
Моро, Волкова, Проверочные работы

Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 13. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы

Страница 85. Вариант 2. Тест 3,
Моро, Волкова, Проверочные работы

Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 36,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1,
Мерзляк, Полонский, Якир, Учебник

Упражнение 520,
Мерзляк, Полонский, Якир, Учебник

Упражнение 656,
Мерзляк, Полонский, Якир, Учебник

Упражнение 657,
Мерзляк, Полонский, Якир, Учебник

Упражнение 673,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1050,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 1211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1222,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1262,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1266,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Как делить в столбик с остатком?

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

Деление с остатком

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

слайд из презентации о делении чисел с остатком

Запишите его в ответе либо:

• как дробь, где в числителе остаток, а в знаменателе — делитель
• словами, например, 73 целых и 6 в остатке

Деление методом последовательного вычитания

Только что мы говорили о делении в контексте умножения. На основе этого знания можно проводить операцию деления. Однако, существует еще один, достаточно простой и достойный внимания подход — деление методом последовательного вычитания. Этот способ понятен интуитивно, поэтому рассмотрим его на примере, не приводя теоретических выкладок.

Заголовок

Сколько будет 12 разделить на 4?

Иными словами данную задачу можно сформулировать так: имеется 12 предметов (например, апельсинов), и их нужно разделить на равные группы по 4 предмета (разложить в коробки по 4 штуки). Сколько будет таких групп или коробок по четыре апельсина в каждой?

Шаг за шагом будем отнимать от исходного количества по 4 апельсина и формировать группы по 4 до того момента, пока апельсины не закончатся. Количество шагов, которые нам придется сделать, и будет ответом на изначальный вопрос.

Из 12 апельсинов откладываем первую четверку в коробку. После этого в исходной куче апельсинов остается 12-4=8цитрусовых. Из этих восьми в другую коробку забираем еще 4. Теперь в исходной куче апельсинов осталось 8-4=4штуки. Из этих четырех штук как раз можно сформировать еще одну, отдельную третью коробку, после чего в исходной куче останется 4-4= апельсинов.

Итак, мы получили 3 коробки, по 4 предмета в каждой. Иными словами, мы разделили 12 на 4, и получили в результате 3. 

Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.

Важно!

При делении методом последовательного вычитания количество операций вычитания до получения нулевого остатка и есть частное от деления.

Для закрепления рассмотрим еще один, более сложный пример.

Пример 1. Деление последовательным вычитанием

Вычислим результат деления числа 108 на 27 методом последовательного вычитания.

Первое действие: 108-27=81.

Второе действие: 81-27=54.

Третье действие: 54-27=27.

Четвертое действие: 27-27=.

Более действий не требуется. Мы получили ответ:

108÷27=4

Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Задачи, которые решаются при помощи действия деления

В курсе математики
средней школы наиболее часто используется деление при решении таких задач,
когда нужно:

• Узнать, во сколько раз одно число меньше и больше другого? Этот вопрос может звучать по-другому: сколько раз меньшее число содержится (помещается) в большем? Или: сколько раз поместится в большем числе меньшее?Например: сколько пятиграммовых стиков сахара находится в килограммовой упаковке? (1000 г : 5 г = 200 шт.).
• Число разделить на заданное количество равных частей.Например: сколько получится грамм сахара в каждом пакете, если пересыпать килограмм сахара в 5 одинаковых пакетов поровну? (1000 г : 5 шт. = 200 г).
• Уменьшить число в заданное количество раз.Например: для приготовления блюда на 5 человек использовали 1 кг сахара, а сколько сахара потребуется для приготовления этого же блюда для одного человека? (1000 г : 5 чел. = 200 г).

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий при делении на двузначные числа. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.

2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.

3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.
После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка.

4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Как разделить одну десятичную дробь на другую: столбиком, умножением

Делим одну десятичную дробь на другую

Для облегчения процесса, мы обязательно множим делимое и делитель на число с нулем: 10, 100, 1000 и числами с большим количеством нулей. Таким образом, делитель автоматически превращается в натуральное число. Потом действия, конечно же, повторяются. Все происходит благодаря свойствам деления и умножения.

Потом обычные числа просто делятся – методично и в столбик. Но помните, что изначально делились именно десятичные дроби. Разделить десятичную дробь на 0,1, 0,01, 0,001 — то же самое, что умножить ее на 10, 100, 1000 соответственно.

Чтобы разделить конечную десятичную дробь на другую, следует:

• Прибегнуть к переносу запятой в делимом и делителе на нужное количество знаков, которое превратит делитель в натуральное число. Если же знаков в делимом будет по каким-то причинам недостаточно, то с правой стороны дописываются необходимые нули.
• Далее просто делим дробь в столбик на то число, которое получилось. Как можно заметить, схема очень логична и элементарна.

Вот примеры решений столбиком:

Примеры с дробями на деление
Примеры с дробями на деление
Примеры с дробями на деление

По этому методу можно разделить натуральное число на десятичную дробь. Вот пример, как это выполняется:

Примеры с дробями на деление

Почему нельзя делить на 0?

Изначально следует заметить, что данная истина в некотором смысле неправильная. В действительности делить на 0 возможно, но у такого примера будет бесконечное число ответов. В чём-то подобное уравнение схоже с числом «Пи», у которого отсутствует конечный результат. Вот почему нельзя делить на ноль, по утверждению школьных учителей, а ученики безоговорочно верят этому.

Школьные учителя вряд ли смогут детям пояснить, в чём суть принципа бесконечности. Легче просто сказать, чтобы ученики взяли за аксиому правило, что делить на это число нельзя. Пусть это не совсем так, но дети не будут стараться решать пример, у которого бесконечное количество ответов. В случае, когда, разбирая задачу, школьник вынужден в решении проводить деление на 0, это означает, что он допустил ошибку.

Как происходит деление?

В действительности при решении такого уравнения можно получить и другой ответ – бесконечность (если расчеты были проведены правильно). В качестве доказательства не придётся прибегать к помощи физических формул. Чаще всего математические доказательства подразумевают решение одной простой задачи, у которой есть бесконечное число ответов.

В качестве примера постараемся разделить 5 на ноль. Любой ученик пятого класса ответит, что у этого примера решение отсутствует. Но нам известно, что это действие можно представить в виде такого уравнения: «0*х=5».

Другими словами, перед нами стоит задача найти число, при умножении которого на ноль получится 5. Но общеизвестно, что, если любое число умножить на ноль, результатом будет 0. Такие свойства цифры являются неотъемлемыми, а любая попытка опровержения аксиомы попросту бессмысленна. Вот почему нельзя делить на ноль, по утверждению школьных учителей. И такой запрет будет существовать и впредь, так как решение примера, где нужно число умножить на 0 и получить что-то, отличающееся от нуля, просто нереально, по крайней мере для школьника.

Но высшая математика позволяет решать примеры с делением на 0. Причем такое уравнение дает большое количество ответов. Такой приём имеет название «принцип бесконечности». Он позволяет доказать существование одного единственного числа, которое делится на 0. Этим числом является сам 0. Попробуем решить такой пример: 0*х=0. Результат получаем такой:

• х=0;
• также ответом может быть любое другое число, к примеру, 379.

Когда х можно заменить каким угодно числом, это означает, что у задачи на деление есть много ответов. Главное условие – один множитель в обратном уравнении должен равняться 0.

Как проводится

Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.

Приведем простой пример того, как делить с остатком:

Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:

5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.

Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.

Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.

Основные этапы:

1. Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
2. Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 помещается, 5*2=10 помещается, 5*3=15 помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
3. Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.

Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Деление с помощью таблицы умножения

Таблица умножения — удобный инструмент, который позволяет найти произведения однозначных натуральных чисел. Однако, ее можно использовать и для деления.

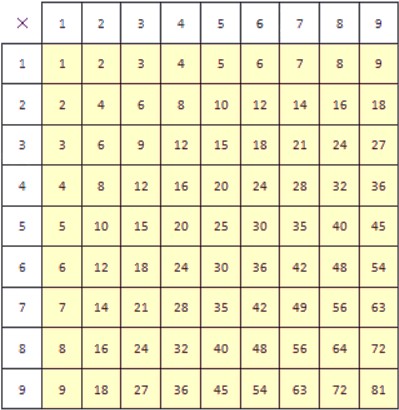
Таблица умножения позволяет находить не только результат произведения множителей, но и множитель по известному произведению и другому множителю. Как мы выяснили ранее, деление — это как раз и есть нахождение неизвестного множителя по известному произведению и еще одному множителю. 

С помощью таблицы умножения можно проводить деление любого числа на желтом фоне на любое однозначное натуральное число. Покажем, как это делать. Есть два способа, применение которых мы будем рассматривать на примерах.

Разделим 48 на 6.

Способ первый.

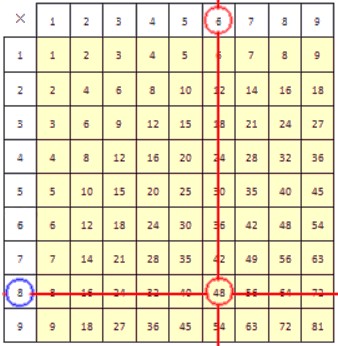
В столбце, верхняя ячейка которого содержит делитель 6, находим делимое 48. Результат деления при этом находится в крайней левой ячейке строки, содержащей делимое. Он обведен синей окружностью.

Способ второй. 

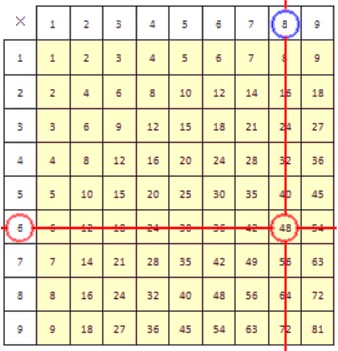
Сначала в строке с делителем 6 находим делимое 48. Результат деления при этом находится в крайней верхней ячейке столбца, содержащем делимое. Он обведен синей окружностью.

Итак, мы разделили 48 на 6 и получили 8. Результат был найден по таблице умножения двумя способами. Оба способа абсолютно идентичны.

Для закрепления рассмотрим еще один пример. Разделим 7 на 1. Приведем рисунки, иллюстрирующие процесс деления.

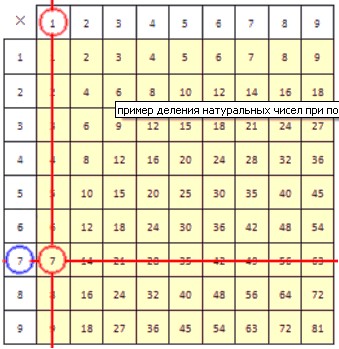
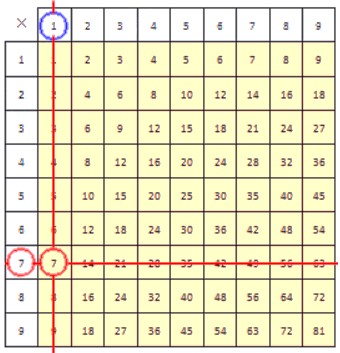
В результате деления числа 7  на  1, как вы уже догадались, получается число 7

В делении с помощью таблицы умножения очень важно знать эту таблицу наизусть, так как не всегда можно иметь ее под рукой

Настоятельно рекомендуем выучить таблицу умножения!