Таблица умножения до 20 и до 100

Помогите вашему ребенку выучить таблицу умножения: с чего начать

Если ваш ребенок уже сталкивался с таблицей умножения — видел, задавал вопросы, пробовал применить

• Объясните сыну или дочке, что такое количество цифр не должно пугать: не придется заучивать все наизусть
• В таблице умножения есть определенные логические закономерности.
• Дайте понять, что вы не собираетесь заставлять бездумно зубрить числа, но поможете увидеть связь между ними.

Если ребенок до этого не видел таблицу

Купите или распечатайте плакат с ней и повесьте над рабочим столом, чтобы школьник привык к ее виду. Даже если ребенок визуально знаком с таблицей, лучше все равно украсить ей детскую зону. Предлагаем несколько таких плакатов для распечатывания.

Примеры плакатов с таблицей умножения

Ребенок сопротивляется или просто не понимает, в чем смысл умножения?

Объясните, что это более короткая запись уже того, что он знает — сложения. Это станет первым шагом к снижению тревожности из-за нового учебного материала.

Покажите, что 2+2 — то же самое, что 2*2, а 3+3+3 можно спокойно заменить на 3*3 и так далее.

Наконец, перед реальными математическими занятиями вместе с ребенком через умножение:

1. Попробуйте считать количество конфет в коробке;
2. Количество предметов в недельном расписании;
3. Количество колес на всех игрушечных машинках или рук и ног у кукол — на что хватит фантазии.

Решение задач с величинами «цена», «количество», «стоимость»

Гномик Чихун знакомит с полезным ископаемым — каменной солью.

Раньше соль очень дорого ценилась, и за один килограмм соли платили серебром.

Для покупок надо знать цену, стоимость и количество вещей, которые хотите купить. Давайте разберемся в этих понятиях.

Задачи с величинами цена, количество, стоимость вычисляйте по формулам.

Решение задачи 1. Известны цена, количество. Найдите стоимость.

Килограмм соли стоит 30 рублей. Сколько стоит два килограмма соли?

Составляем таблицу. В задаче три величины, поэтому начертите три столбца и две строки:

Задание 2. Составьте обратную задачу на нахождение цены.

Проверьте:

Два килограмма соли стоят 60 рублей. Сколько стоит 1 килограмм соли?

Эта задача на нахождение цены. Решаем задачу по формуле Ц = С : К, данные занесите в таблицу.

Задача 3. Известна цена и стоимость. Найдите количество.

Таблица умножения на 60 до 150

60 x 141 = 8460(шестьдесят умножить на сто сорок один равно восемь тысяч четыреста шестьдесят)

60 x 142 = 8520(шестьдесят умножить на сто сорок два равно восемь тысяч пятьсот двадцать)

60 x 143 = 8580(шестьдесят умножить на сто сорок три равно восемь тысяч пятьсот восемьдесят)

60 x 144 = 8640(шестьдесят умножить на сто сорок четыре равно восемь тысяч шестьсот сорок)

60 x 145 = 8700(шестьдесят умножить на сто сорок пять равно восемь тысяч семьсот)

60 x 146 = 8760(шестьдесят умножить на сто сорок шесть равно восемь тысяч семьсот шестьдесят)

60 x 147 = 8820(шестьдесят умножить на сто сорок семь равно восемь тысяч восемьсот двадцать)

60 x 148 = 8880(шестьдесят умножить на сто сорок восемь равно восемь тысяч восемьсот восемьдесят)

60 x 149 = 8940(шестьдесят умножить на сто сорок девять равно восемь тысяч девятьсот сорок)

60 x 150 = 9000(шестьдесят умножить на сто пятьдесят равно девять тысяч)

Таблица умножения на 6

Таблица умножения на 6

С умножением на «6» появляются первые трудности: действия запоминаются сложно, а цифры получаются большими.

Таблица умножения на 6:

6х1=6   (6 повторяется 1 раз — получается 6)

6х2=12   (6 повторяется 2 раза — получается 12)

6х3=18   (6 повторяется 3 раза — получается 18)

6х4=24   (6 повторяется 4 раза — получается 24)

6х5=30   (6 повторяется 5 раз — получается 30)

6х6=36   (6 повторяется 6 раз — получается 36)

6х7=42   (6 повторяется 7 раз — получается 42)

6х8=48   (6 повторяется 8 раз — получается 48)

6х9=54   (6 повторяется 9 раз — получается 54)

6х10=60   (6 повторяется 10 раз — получается 60)

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

3 × 5 = 15

Теперь поменяем местами сомножители:

5 × 3 = 15

В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

3 × 5 = 5 × 3

15 = 15

А с помощью  переменных переместительный закон умножения можно записать так:

a × b = b × a

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

24 = 24

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

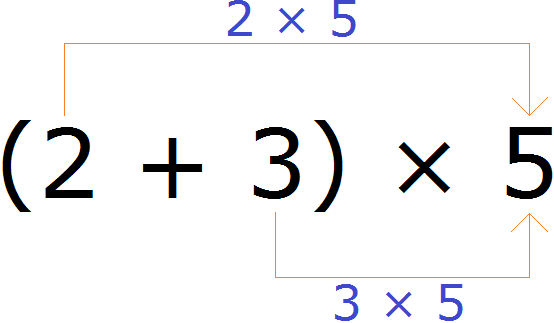
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25.

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

0 × 2 = 0

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

0 × 2 = 2 × 0

0 = 0

Примеры применения закона умножения на ноль:

5 × 0 = 0

5 × 5 × 5 × 0 = 0

2 × 5  × 0 × 9  × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.

Таблица умножения на 6 до 70

Закрепление таблицы умножения на 6 6 x 61 = 366(шесть умножить на шестьдесят один равно триста шестьдесят шесть)

6 x 62 = 372(шесть умножить на шестьдесят два равно триста семьдесят два)

6 x 63 = 378(шесть умножить на шестьдесят три равно триста семьдесят восемь)

6 x 64 = 384(шесть умножить на шестьдесят четыре равно триста восемьдесят четыре)

6 x 65 = 390(шесть умножить на шестьдесят пять равно триста девяносто)

6 x 66 = 396(шесть умножить на шестьдесят шесть равно триста девяносто шесть)

6 x 67 = 402(шесть умножить на шестьдесят семь равно четыреста два)

6 x 68 = 408(шесть умножить на шестьдесят восемь равно четыреста восемь)

6 x 69 = 414(шесть умножить на шестьдесят девять равно четыреста четырнадцать)

Как выучить ребенку таблицу умножения легко и быстро.

1. Умножение на 1 и 10.

 1 х1  – это значит, нужно единицу взять один раз. Получим 1 х1 = 1.

1 х 2 – это значит, нужно единицу взять два раза. Получим 1 х2 = 2. И т.д.

Аналогично, для числа 10.

10 х 1 – это значит, нужно десятку взять один раз. Получим 10 х1 = 10.

10 х 2 – это значит, нужно десятку взять два раза. Получим 10 х2 = 20. И т д.

2. Умножение на 2.

Умножить число на 2 – это значит его удвоить, то есть сложить с самим собой: 5 х 2 = 5 +5 =10 или 9 х 2 = 9 + 9 = 18.

3. Умножение на 4 и 8.

Этот процесс связан с предыдущим, так как 4 = 2 х 2, а 8 = 4 х 2 = 2 х2 х 2. Это значит, чтобы умножить число на 4, нужно сначала это число удвоить, а потом результат еще раз удвоить.

Например, 6 х 4 = (6 х 2)  х 2 = 12  х 2 = 24.

Аналогично, с умножением на 8: только удваивать нужно три раза.

Пример: 5 х 8 =( (5 х 2)  х 2) х 2 = 40.

Умножение на 3 и 6.

Для запоминания таблицы умножения на 3 и 6 можно порекомендовать стихи Марины Казариной:

Умножение на 5.

Учитывая , что 10 = 5 х 2, легко умножать число сначала на 10, а потом делить на 2.

Пример: 6 х 5 = (6 х 10) : 2 = 30.

Сначала посчитаем 6 х 10 = 60, а затем результат  разделим на  два:  60 : 2 = 30. Значит, 6 х 5 = 30.

Умножение на 7.

Все предыдущие пункты включают в себя уже умножение на 7.  Так, мы знаем уже, что 2 х 7  – это значит семерку удвоить.  5 х 7 – это значит 70:2 = 35.

Осталось два примера на 7 , один из которых нужно просто запомнить и все: 7 х 7 = 49. А второй 7 х 9 мы рассмотрим ниже как  пример 9 х 7.

Умножение на 9.

Здесь учитываем то, что 9 = 10 – 1.

Поэтому, чтобы умножить число на 9 , достаточно к числу приписать справа ноль и вычесть само это  число.

Пример : 8 х 9 = 8 0 – 8  = 72.

А вот еще один способ умножения на число 9 (что называется, показываем на пальцах).

Таблица умножения на 3

Таблица умножения на 3

Объясните ребенку на наглядном примере, как происходит умножение на «3», чтобы он понял. Тогда у него получится быстро запомнить это действие.

Таблица умножения на 3

3х1=3   (3 повторяется 1 раз — получается 3)

3х2=6   (3 повторяется 2 раза — получается 6)

3х3=9   (3 повторяется 3 раза — получается 9)

3х4=12   (3 повторяется 4 раза — получается 12)

3х5=15   (3 повторяется 5 раз — получается 15)

3х6=18   (3 повторяется 6 раз — получается 18)

3х7=21   (3 повторяется 7 раз — получается 21)

3х8=24   (3 повторяется 8 раз — получается 24)

3х9=27   (3 повторяется 9 раз — получается 27)

3х10=30   (3 повторяется 10 раз — получается 30)

Таблица умножения на 16 до 150

16 x 141 = 2256(шестнадцать умножить на сто сорок один равно две тысячи двести пятьдесят шесть)

16 x 142 = 2272(шестнадцать умножить на сто сорок два равно две тысячи двести семьдесят два)

16 x 143 = 2288(шестнадцать умножить на сто сорок три равно две тысячи двести восемьдесят восемь)

16 x 144 = 2304(шестнадцать умножить на сто сорок четыре равно две тысячи триста четыре)

16 x 145 = 2320(шестнадцать умножить на сто сорок пять равно две тысячи триста двадцать)

16 x 146 = 2336(шестнадцать умножить на сто сорок шесть равно две тысячи триста тридцать шесть)

16 x 147 = 2352(шестнадцать умножить на сто сорок семь равно две тысячи триста пятьдесят два)

16 x 148 = 2368(шестнадцать умножить на сто сорок восемь равно две тысячи триста шестьдесят восемь)

16 x 149 = 2384(шестнадцать умножить на сто сорок девять равно две тысячи триста восемьдесят четыре)

16 x 150 = 2400(шестнадцать умножить на сто пятьдесят равно две тысячи четыреста)

Таблица умножения на 60 до 30

Математика таблица умножения на 60 60 x 21 = 1260(шестьдесят умножить на двадцать один равно одна тысяча двести шестьдесят)

60 x 22 = 1320(шестьдесят умножить на двадцать два равно одна тысяча триста двадцать)

60 x 23 = 1380(шестьдесят умножить на двадцать три равно одна тысяча триста восемьдесят)

60 x 24 = 1440(шестьдесят умножить на двадцать четыре равно одна тысяча четыреста сорок)

60 x 25 = 1500(шестьдесят умножить на двадцать пять равно одна тысяча пятьсот)

60 x 26 = 1560(шестьдесят умножить на двадцать шесть равно одна тысяча пятьсот шестьдесят)

60 x 27 = 1620(шестьдесят умножить на двадцать семь равно одна тысяча шестьсот двадцать)

60 x 28 = 1680(шестьдесят умножить на двадцать восемь равно одна тысяча шестьсот восемьдесят)

60 x 29 = 1740(шестьдесят умножить на двадцать девять равно одна тысяча семьсот сорок)

Вы здесь

Таблица умножения и деления

Файлы: 

Вложение	Размер
Таблица умножения и деления, картинка с пояснением	74.46 КБ
Таблица умножения и деления	105.44 КБ
Таблица умножения и деления без ответов	19.53 КБ

Чтобы скачать и рапсечатать таблицу умножения и деления, используйте ссылки выше или нажмите правую кнопку мышки над картинками ниже и выберите «сохранить картинку как».

Таблица умножения и деления без ответов.

Тип:

материал

• Все тесты. Проверка. Тренажер таблицы умножения.
  • Умножение на 1. Все тесты.
    • Умножение на 1 (ввести ответ
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (найти ответ
    • Умножение на 1 (найти ответ
  • Умножение на 2. Все тесты.
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (найти ответ
    • Умножение на 2 (найти ответ
  • Умножение на 3. Все тесты.
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (найти ответ
    • Умножение на 3 (найти ответ
  • Умножение на 4. Все тесты.
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (найти ответ
    • Умножение на 4 (найти ответ
  • Умножение на 5. Все тесты.
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (найти ответ
    • Умножение на 5 (найти ответ
  • Умножение на 6. Все тесты.
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (найти ответ
    • Умножение на 6 (найти ответ
  • Умножение на 7. Все тесты.
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (найти ответ
    • Умножение на 7 (найти ответ
  • Умножение на 8. Все тесты.
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (найти ответ
    • Умножение на 8 (найти ответ
  • Умножение на 9. Все тесты.
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (найти ответ
    • Умножение на 9 (найти ответ
  • Умножение на 10. Все тесты.
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (найти ответ
    • Умножение на 10 (найти ответ
  • Тест-тренажер онлайн! Таблица умножения
  • Тест-тренажер онлайн! Таблица умножения. 10 вопросов.
• Умножение
  • Умножение на 1
  • Умножение на 2
  • Умножение на 3
  • Умножение на 4
  • Умножение на 5
  • Умножение на 6
  • Умножение на 7
  • Умножение на 8
  • Умножение на 9
  • Умножение на 10
• Таблица умножения до 20 и до 100
• Таблица умножения и деления
• Умножение в столбик
• Еще
  • Таблица сложения
  • Линейка
  • Без ответов
  • Таблица кубов
  • Таблица степеней
  • Калькуляторы
    • Умножение
    • Найти неизвестный множитель
    • Деление
    • Сложение
    • Кубов
  • Шпаргалка

Таблица умножения на 7

Таблица умножения на 7

Седьмой столбец таблицы умножения обычно запоминается легче, чем последующие. В нем есть пару сложных действий, которые нужно заучить.

Таблица умножения на 7:

7х1=7   (7 повторяется 1 раз — получается 7)

7х2=14   (7 повторяется 2 раза — получается 14)

7х3=21   (7 повторяется 3 раза — получается 21)

7х4=28   (7 повторяется 4 раза — получается 28)

7х5=35   (7 повторяется 5 раз — получается 35)

7х6=42   (7 повторяется 6 раз — получается 42)

7х7=49   (7 повторяется 7 раз — получается 49)

7х8=56   (7 повторяется 8 раз — получается 56)

7х9=63   (7 повторяется 9 раз — получается 63)

7х10=70   (7 повторяется 10 раз — получается 70)

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел Деление на нуль невозможно. Деление нуля на число: 0 : a = 0. Деление равных чисел: a : a = 1. Деление на единицу: a : 1 = a. Для деления переместительное свойства не выполняется: a : b ≠ b : a. Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c). Деление произведения на число:(a * b) : c = (a : c) * b, если a делится на c; (a * b) : c = a * (b : с), если b делится на c;(a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c. Деление числа на произведение: a : (b * c) = (a : b) * (1 : c) = (a : c) * (1 : b).

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?

Как решаем:

Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.

Ответ: 2 кг

Пример 2

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 3

Упростить выражение: 27a – 16a.

Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.

Ответ: 11a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Таблица умножения на 9

Таблица умножения на 9

Девятый столбец является одним из самых легких. На «9» мы умножали уже все числа. Поэтому малышу придется выучить только одно действие: 9х9

Таблица умножения на 9:

9х1=9   (9 повторяется 1 раз — получается 9)

9х2=18   (9 повторяется 2 раза — получается 18)

9х3=27   (9 повторяется 3 раза — получается 27)

9х4=36   (9 повторяется 4 раза — получается 36)

9х5=45   (9 повторяется 5 раз — получается 45)

9х6=54   (9 повторяется 6 раз — получается 54)

9х7=63   (9 повторяется 7 раз — получается 63)

9х8=72   (9 повторяется 8 раз — получается 72)

9х9=81   (9 повторяется 9 раз — получается 81)

9х10=90   (9 повторяется 10 раз — получается 90)

Таблица умножения с помощью пальцев на 6, 7 и 8: схемы с подробным описанием

Подготовим правильное положение рук

Первым делом нужно, чтобы руки ребенка приняли правильную позицию. Для этого поставим их перед собой, развернув ладонями к лицу. При этом старайтесь немного их направить в сторону друг друга, поскольку работать нужно будет по методу касания пальцев. То есть, мизинцы должны находиться внизу. На каждой руке пальцы будут обозначать одни и те же цифры:

Большой палец, как задорный толстяк,

Пусть носит звание – 10-й добряк!

Указательный, да господин влиятельный

Солнечной 9-ой опознавательный.

Средний палец – хулиган

В бесконечную 8-ку зван!

Безымянный, который окольцованный,

Еще и магической 7-ой заколдованный!

Наш любимец – малой мизинец

Получил 6-ой гостинец!

Таким образом, мы подготовились к умножению на пальцах. Далее выбираем пример, который хотим решить.

Дайте пальцам не только счет, но и прозвища

Рассмотрим пример таблицы умножения 6 на 7

• Цифру 6 на левой руке у нас означает мизинец, а цифру 7 – безымянный палец, но на правой руке.
• Нам нужно соединить их вместе, соприкасаясь стыками подушечек. При таком соприкосновении другие пальцы остаются свободными.

Дабы усвоить материал, предлагаем вернуться к нашему примеру:

1. На левой руке у нас только один палец, что с шестым гостинцем. Он у нас в соединении.
2. На правой руке уже два пальца – мизинец, что внизу конструкции, и безымянный, который в стыке с левой рукой.

Умножение 6 на 7

• Таким образом, в числе нашего результата в разряде десятков будет стоять цифра 3. То есть, три пальца означают 30. На фото имеют голубой цвет. 
• А чтобы узнать цифру разряда единиц, нужно сосчитать по отдельности оставшиеся свободные пальцы на обеих руках и перемножить их между собой. Они пронумерованы синим цветом на верхнем фото.
• В нашем случае:
  • На левой руке остались свободными 4 пальца – толстяк, господин, хулиган и безымянный
  • На правой руке остались свободными 3 пальца – средний и указательный, а также большой
• Нам нужно 3 умножить на 4. Таким образом, мы получили цифру разряда единиц – это 12.
• В завершение к 30 добавляем наши 12-е единицы и получаем 42!

Может быть вариант еще намного проще, когда при умножении верхних свободных пальцев для получения цифры разряда единиц результат получается меньше 9. В таком случае сложить вместе два числа куда проще даже первоклассникам.

Если ваш малыш еще не до автоматизма усвоил материал, тогда разбейте суммирование на этапы:

• 3 – это десятки
• Число 12 – это 1 десяток и 2 единицы
• В итоге мы складываем 3+1, получаем 4 десятка
• А к ним уже добавляем оставшиеся 2 единицы
• И получаем 42
• Результатом умножения 6 на 7 или 7 на 6, поскольку разницы никакой нет, будет число 42.

Небольшая проверка на внимательность

Рассмотрим пример таблицы умножения 7 на 10

Несмотря на простоту такого умножения, у детворы порой возникают трудности с пониманием самой схемы. Поэтому такой простой пример стоит рассматривать после базового разбора пальцевой методики. Нумеровать пальцы нужно точно в такой же последовательности:

• цифру 7 означает безымянный палец левой руки
• а цифру 10 – большой толстяк

И теперь мы состыковываем большой палец с безымянным.

Умножение 7 на 10

• Таким образом, для получения цифры разряда десятков нужно прибавить к двум пальцам левой руки все пять фаланг правой. В итоге мы получаем цифру 7. То есть, 70.
• Для получения цифры разряда единиц нужно 4 свободных пальца левой руки умножить на 0 свободных пальцев правой руки. В результате получаем 0.
• В итоге к 70 мы добавляем 0, но получаем те же 70. Перепроверяем результат!

Таблица умножения на 8: пример 8 на 8

1. Состыковываем наши средние пальцы, поскольку они отвечают за цифру 8.

Умножаем 8 на 8

1. Внизу у нас по 2 пальца на каждой руке и еще 2 в замке. В итоге мы имеем 6 пальцев. То есть, 60.
2. Вверху конструкции осталось 4 свободных пальца. То есть, мы умножаем 2 на 2 и получаем 4. Достаточно просто, ведь их можно и сложить, и умножить, а получить один и тот же результат.
3. В итоге к 6 десяткам мы добавляем 4 и получаем 64!

Как учить ребенка учиться

Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.

А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.

Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.

Таблица умножения на 6 до 120

Занимательная таблица умножения на 6 6 x 111 = 666(шесть умножить на сто одиннадцать равно шестьсот шестьдесят шесть)

6 x 112 = 672(шесть умножить на сто двенадцать равно шестьсот семьдесят два)

6 x 113 = 678(шесть умножить на сто тринадцать равно шестьсот семьдесят восемь)

6 x 114 = 684(шесть умножить на сто четырнадцать равно шестьсот восемьдесят четыре)

6 x 115 = 690(шесть умножить на сто пятнадцать равно шестьсот девяносто)

6 x 116 = 696(шесть умножить на сто шестнадцать равно шестьсот девяносто шесть)

6 x 117 = 702(шесть умножить на сто семнадцать равно семьсот два)

6 x 118 = 708(шесть умножить на сто восемнадцать равно семьсот восемь)

6 x 119 = 714(шесть умножить на сто девятнадцать равно семьсот четырнадцать)

Как быстро и легко выучить таблицу умножения с ребёнком?

Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.

Совет №1

Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.

Умножение – это сумма одинаковых слагаемых.

8 умножить на 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8

Понимая смысл умножения, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.

Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.

Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее:   4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32

Умножать можно с помощью рук

Умножение на 9

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.

Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

Способ 2

Например, нужно умножить 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Совет № 3

Знание правил умножения упростит запоминание таблицы умножения:

• При умножении любого числа на 1 получается то число, которое умножали.
• Все результаты умножения на 10 начинаются с числа, которое мы умножаем, а заканчиваются на 0.
• Все результаты умножения на 5 заканчиваются на 5 или 0: если умножали нечётное число – на 5, если чётное – на 0.
• Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 на 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
• При умножении на 9, запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.

Научиться пользоваться таблицей Пифагора

Необходимо показать ребёнку, что числа из левого столбика умножаются на числа из верхней строки. Найти результат очень просто: нужно только провести рукой по таблице вниз и вправо от множителей до места пересечения, где и будет расположен результат умножения.

Возьмите пустую распечатанную или нарисованную таблицу и заполните её вместе с ребёнком. Причем в цвете, закрашивая одинаковый результат одним цветом. Сразу будет видна закономерность. Ребёнок увидит, что запоминать нужно только половину таблицы (согласно переместительному закону умножения).

Понимая смысл умножения, можно использовать для вычислений предыдущие или последующие табличные случаи. При этом случае нужно лишь вычесть или прибавить нужное число.