Распечатать

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

• Единица (1) — самое маленькое число, а самого большого числа не существует.
• Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Таблица умножения на 4

Таблица умножения на 4

Четвертый столбик таблицы умножения еще легкий и ребенок без труда запомнит его. Помогите малышу своими подсказками и поддержкой в виде слов подбадривания и похвалы, и он обязательно все сможет.

Таблица умножения на 4

4х1=4   (4 повторяется 1 раз — получается 4)

4х2=8   (4 повторяется 2 раза — получается 8)

4х3=12   (4 повторяется 3 раза — получается 12)

4х4=16   (4 повторяется 4 раза — получается 16)

4х5=20   (4 повторяется 5 раз — получается 20)

4х6=24   (4 повторяется 6 раз — получается 24)

4х7=28   (4 повторяется 7 раз — получается 28)

4х8=32   (4 повторяется 8 раз — получается 32)

4х9=36   (4 повторяется 9 раз — получается 36)

4х10=40   (4 повторяется 10 раз — получается 40)

Тренажер по таблице умножения и деления

Бесценный богатый тренажер!
В книге вы найдете:

•  страницы интересных результативных упражнений;
• разнообразные задания;
• творческий подход;
• нестандартные приемы;
• задания разного уровня сложности;
• различные шифровки;
• игры и раскраски.
• Ваш ребенок получит:

легкое и без нервов запоминание таблицы умножения;
развитие внимания и мышления;
улучшение в целом математических способностей;
огромное количество интересных и полезных заданий.
Книга может быть использована как для индивидуальной работы, так и работы в классе.
Скучно точно не будет!

Тренажер удобен для распечатывания!

Таблица умножения на 7 до 40

Таблица умножения на 7 ответы 7 x 31 = 217(семь умножить на тридцать один равно двести семнадцать)

7 x 32 = 224(семь умножить на тридцать два равно двести двадцать четыре)

7 x 33 = 231(семь умножить на тридцать три равно двести тридцать один)

7 x 34 = 238(семь умножить на тридцать четыре равно двести тридцать восемь)

7 x 35 = 245(семь умножить на тридцать пять равно двести сорок пять)

7 x 36 = 252(семь умножить на тридцать шесть равно двести пятьдесят два)

7 x 37 = 259(семь умножить на тридцать семь равно двести пятьдесят девять)

7 x 38 = 266(семь умножить на тридцать восемь равно двести шестьдесят шесть)

7 x 39 = 273(семь умножить на тридцать девять равно двести семьдесят три)

Помогите вашему ребенку выучить таблицу умножения: с чего начать

Если ваш ребенок уже сталкивался с таблицей умножения — видел, задавал вопросы, пробовал применить

• Объясните сыну или дочке, что такое количество цифр не должно пугать: не придется заучивать все наизусть
• В таблице умножения есть определенные логические закономерности.
• Дайте понять, что вы не собираетесь заставлять бездумно зубрить числа, но поможете увидеть связь между ними.

Если ребенок до этого не видел таблицу

Купите или распечатайте плакат с ней и повесьте над рабочим столом, чтобы школьник привык к ее виду. Даже если ребенок визуально знаком с таблицей, лучше все равно украсить ей детскую зону. Предлагаем несколько таких плакатов для распечатывания.

Примеры плакатов с таблицей умножения

Ребенок сопротивляется или просто не понимает, в чем смысл умножения?

Объясните, что это более короткая запись уже того, что он знает — сложения. Это станет первым шагом к снижению тревожности из-за нового учебного материала.

Покажите, что 2+2 — то же самое, что 2*2, а 3+3+3 можно спокойно заменить на 3*3 и так далее.

Наконец, перед реальными математическими занятиями вместе с ребенком через умножение:

1. Попробуйте считать количество конфет в коробке;
2. Количество предметов в недельном расписании;
3. Количество колес на всех игрушечных машинках или рук и ног у кукол — на что хватит фантазии.

Механический рычаг, момент силы

О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.

Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы.

Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.

Порядок выполнения действий

Простак гуляет, улыбается, считает, веселит друзей. У него свой способ выполнения действий. Он много знает, но не разговаривает, а показывает жестами.

У каждого из нас собственная программа выполнения действий. Иногда расписание меняется, но некоторый порядок менять нельзя. Вы просыпаетесь утром, сначала делаете зарядку, после убираете спальное место. А случается так — сразу застилаете постель, а зарядку выполняете только днем. Но выйти зимой на улицу без обуви и пальто вы не можете, поэтому всегда сначала одеваетесь, лишь потом идете гулять. Гномы перед поиском полезных ископаемых обязательно завтракают.

Нужны ли в математике правила порядка выполнения определенных действий? Простак показал жестом, что примеры со сложением и вычитанием надо решать слева направо, а не наоборот. Нарушение порядка дает неверный ответ.

Порядок выполнения действий друг за другом.

Ниже в примере встречаются все основные виды арифметических операций. По правилу умножение и деление решаются раньше, чем сложение и вычитание. Поэтому первым действием разделим пятнадцать на три, затем умножим шесть на четыре.

В математике есть способ, который показывает, что решается раньше других действий. Нарисуйте скобки — выполните первым вычитание.

Как найти правильный ответ в таких примерах:

Сначала решайте выражения, записанные в скобках;

Далее действия второй ступени — умножение и деление по порядку;

А первой ступени — сложение и вычитание решайте последними действиями.

Алгоритм выполнения действий запишите схемой:

Будьте внимательны к выполнению порядка, чтобы не допускать ошибки.

Ребята, наше путешествие подошло к концу. Гномики прощаются с вами и желают учиться на «отлично».

До скорой встречи!

ДИНАМИКА. Теория и формулы (кратко).

Динамика – раздел физики, изучающий причины движения тел.

Первый закон Ньютона утверждает, что существуют инерциальные системы отсчёта, относительно которых тела сохраняют скорость постоянной, если на них не действуют другие тела.

Второй закон Ньютона утверждает, что ускорение, приобретаемое телом под действием силы, прямо пропорционально модулю силы и обратно пропорционально массе тела.

Третий закон Ньютона утверждает, что взаимодействующие тела действуют друг на друга с силами, векторы которых равны по модулю и противоположны по направлению.

Закон всемирного тяготения гласит: сила гравитационного притяжения двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Коэффициентом пропорциональности служит гравитационная постоянная.

Закон Гука устанавливает пропорциональность модуля силы упругости модулю удлинения тела, если его деформация является упругой. Коэффициентом пропорциональности служит коэффициент жёсткости тела.

Закон Амонтона-Кулона устанавливает пропорциональность силы трения скольжения или максимальной силы трения покоя силе нормальной реакции опоры. Коэффициентом пропорциональности служит коэффициент трения.

Импульсом силы называют произведение вектора скорости на интервал времени её действия. Единица модуля импульса силы – 1 кг·м/c.

Импульсом тела (количеством движения) называют произведение массы тела на вектор его скорости. Единица модуля импульса тела – 1 кг·м/c.

Закон сохранения импульса гласит: сумма импульсов тел до их взаимодействия равна сумме импульсов этих же тел после взаимодействия, если система замкнута.

Изменение кинетической энергии тела равно работе равнодействующей всех сил. Кинетическая энергия тела, перемещающегося в пространстве без вращения, равна половине произведения его массы на квадрат скорости. Единица для измерения – 1 Дж.

Изменение потенциальной энергии тела равно взятой с противоположным знаком работе рассматриваемой потенциальной силы. Потенциальная энергия при действии силы тяжести равна произведению модуля силы тяжести на расстояние от тела до выбранного нулевого уровня энергии. Потенциальная энергия при действии силы упругости равна половине произведения коэффициента жёсткости на квадрат удлинения тела по сравнению с его недеформированным состоянием. Единица для измерения потенциальной энергии любого вида – 1 Дж.

Динамика. Таблицы.

1 файл(ы) 350.35 KB

Конспект по физике «Динамика. Теория и формулы для ЕГЭ» + шпаргалка.

Еще конспекты для 10-11 классов:

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Как быстро и легко выучить таблицу умножения с ребёнком?

Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.

Совет в запоминании №1

Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.

Умножение – это сумма одинаковых слагаемых.

8 x 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8

Понимая смысл множителя, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.

Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.

Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32

Умножать можно с помощью рук Умножение на 9

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.

Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

Способ 2

Например, нужно выяснить сколько будет при счете 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Сводные таблицы

÷1

Делимое	÷	Делитель	Частное(Результат)
1	÷	1	=	1
2	÷	1	=	2
3	÷	1	=	3
4	÷	1	=	4
5	÷	1	=	5
6	÷	1	=	6
7	÷	1	=	7
8	÷	1	=	8
9	÷	1	=	9
10	÷	1	=	10

÷2

Делимое	÷	Делитель	Частное(Результат)
2	÷	2	=	1
4	÷	2	=	2
6	÷	2	=	3
8	÷	2	=	4
10	÷	2	=	5
12	÷	2	=	6
14	÷	2	=	7
16	÷	2	=	8
18	÷	2	=	9
20	÷	2	=	10

÷3

Делимое	÷	Делитель	Частное(Результат)
3	÷	3	=	1
6	÷	3	=	2
9	÷	3	=	3
12	÷	3	=	4
15	÷	3	=	5
18	÷	3	=	6
21	÷	3	=	7
24	÷	3	=	8
27	÷	3	=	9
30	÷	3	=	10

÷4

Делимое	÷	Делитель	Частное(Результат)
4	÷	4	=	1
8	÷	4	=	2
12	÷	4	=	3
16	÷	4	=	4
20	÷	4	=	5
24	÷	4	=	6
28	÷	4	=	7
32	÷	4	=	8
36	÷	4	=	9
40	÷	4	=	10

÷5

Делимое	÷	Делитель	Частное(Результат)
5	÷	5	=	1
10	÷	5	=	2
15	÷	5	=	3
20	÷	5	=	4
25	÷	5	=	5
30	÷	5	=	6
35	÷	5	=	7
40	÷	5	=	8
45	÷	5	=	9
50	÷	5	=	10

÷6

Делимое	÷	Делитель	Частное(Результат)
6	÷	6	=	1
12	÷	6	=	2
13	÷	6	=	3
24	÷	6	=	4
30	÷	6	=	5
36	÷	6	=	6
42	÷	6	=	7
48	÷	6	=	8
54	÷	6	=	9
60	÷	6	=	10

÷7

Делимое	÷	Делитель	Частное(Результат)
7	÷	7	=	1
14	÷	7	=	2
21	÷	7	=	3
28	÷	7	=	4
35	÷	7	=	5
42	÷	7	=	6
49	÷	7	=	7
56	÷	7	=	8
63	÷	7	=	9
70	÷	7	=	10

÷8

Делимое	÷	Делитель	Частное(Результат)
8	÷	8	=	1
16	÷	8	=	2
24	÷	8	=	3
32	÷	8	=	4
40	÷	8	=	5
48	÷	8	=	6
56	÷	8	=	7
64	÷	8	=	8
72	÷	8	=	9
80	÷	8	=	10

÷9

Делимое	÷	Делитель	Частное(Результат)
9	÷	9	=	1
18	÷	9	=	2
27	÷	9	=	3
36	÷	9	=	4
45	÷	9	=	5
54	÷	9	=	6
63	÷	9	=	7
72	÷	9	=	8
81	÷	9	=	9
90	÷	9	=	10

÷10

Делимое	÷	Делитель	Частное(Результат)
10	÷	10	=	1
20	÷	10	=	2
30	÷	10	=	3
40	÷	10	=	4
50	÷	10	=	5
60	÷	10	=	6
70	÷	10	=	7
80	÷	10	=	8
90	÷	10	=	9
100	÷	10	=	10

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.

Разрядные единицы обозначают так:

• Единицы — единицами первого разряда (или простыми единицами) и пишут на первом месте справа.
• Десятки — единицами второго разряда и записывают в числе на втором месте справа.
• Сотни — единицами третьего разряда и записывают на третьем месте справа.
• Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа.
• Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа.
• Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!

Физика 7: все формулы и определения

«Физика 7: все формулы и определения» — это Справочник по физике в 7 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 3-х страницах) и МЕЛКО (формат JPG, на 1-й странице).

1 файл(ы) 255.55 KB

Физика 7 класс: все формулы и определения МЕЛКО на одной странице

1 файл(ы) 549.72 KB

В пособии «Физика 7: все формулы и определения» представлено 24 формулы
и определения за весь курс Физики 7 класса:

Название формулы (закона, правила)	Формулировка закона (правила)	Формула
1. Цена деления шкалы прибора	Для определения цены деления (ЦД) шкалы прибора необходимо: 1) из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N); 2) найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).	ЦД = (ВГ — НГ) / N ЦД = (Б — А) / n
2. Скорость	Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t).	ʋ = S / t
3. Путь	Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.	S = ʋ*t
4. Время движения	Время движения (t) равно отношению пути (S), пройденного телом, к скорости (ʋ) движения.	t = S / ʋ
5. Средняя скорость	Средняя скорость (ʋср) равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (t1 + t2+ t3+ …), за который этот путь пройден.	ʋср = (S1 + S2 + S3 + …) / (t1 + t2 + t3 + …)
6. Сила тяжести	Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (g) — постоянную величину для Земли. (g = 9,8 H/кг)	FТ = m*g
7. Вес	Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (g).	Р = m*g
8. Масса	Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g).	т = Р / g
9. Плотность	Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (т) вещества к его объёму (V).	ρ = m / V
10. Момент силы	Момент силы (М) равен произведению силы (F) на сё плечо (l)	М = F*l
11. Условие равновесия рычага	Рычаг находится в равновесии, если плечи (l1, l2) действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил.	a) F1 / F2 = l1 / l2 б) F1*l1 = F2*l2
12. Давление	Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности	p = F / S
13. Сила давления	Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S)	F = р*S
14. Давление однородной жидкости	Давление жидкости (р) на дно сосуда зависит только от её плотности (ρ) и высоты столба жидкости (h).	p = g ρ h
15.Закон Архимеда	На тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела.	FВ = ρ*g*Vт
16. Условие плавания тел	Если архимедова сила (FВ) больше силы тяжести (FТ) тела, то тело всплывает.	FВ> FТ
17. Закон гидравлической машины	Силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропорциональны площадям (S1, S2) этих поршней.	F1 / F2 = S1 / S2
18. Закон сообщаю-щихся сосудов	Однородная жидкость в сообщающихся сосудах находится на одном уровне (h)	h = const
19. Механическая работа	Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло.	А = F*S
20. Коэффициент полезного действия механизма (КПД)	Коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП).	ɳ = АП / АВ *100%
21. Потенциальная энергия	Потенциальная энергия (ЕП) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (h) над Землей.	ЕП = m*g*h
22. Кинетическая энергия	Кинетическая энергия (ЕК) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ2).	ЕК = m*ʋ2 / 2
23. Сохранение и превращение механической энергии	Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается постоянной.	EП + EК = const
24. Мощность	Мощность (N) — величина, показывающая скорость выполнения работы и равная:а) отношению работы (А) ко времени (t), за которое она выполнена;б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения.	N = A / t N = F*ʋ

12 (двенадцать) самых необходимых (самых востребованных) формул по физике в 7 классе:

Как быстро выучить таблицу деления?

Как быстро выучить таблицу деления?
Таблица деления

Итак, как быстро выучить таблицу деления:

• Не нужно заставлять малыша «зубрить» действия. Он должен понять алгоритм
• Используйте для объяснения монеты или счетные палочки. При помощи этих предметов ребенок сможет не только усвоить деление, но и развить мелкую моторику рук, что хорошо сказывается на мозговой деятельности
• Начните учить таблицу деления с 9. Когда вы дойдете до 5, сложная половина таблицы будет выучена — остальное запомнится легко
• Хвалите малыша и поощряйте его любимыми сладостями, ведь он старается
• Занятия проводите ежедневно. Это поможет развить зрительную память
• Сначала ребенку будет сложно запоминать действия, но со временем он будет давать правильный ответ
• Тренируйте память малыша даже во время прогулки. Например, пусть он посчитает, по сколько конфет было куплено для каждого члена семьи

Скачать бесплатно таблицу умножения: PDF, PNG — 3mu.ru

Все знают, что таблица умножения — это азы всех математических знаний современного человека

Поэтому так важно, чтобы школьник ее выучил как можно раньше. Многие помнят, как на каждой тетрадке в клетку, с обратной стороны печаталась такая таблица

И не просто так, чем чаще к ней обращается ребенок, тем быстрее он научится считать большие примеры.

СПИСОК ТАБЛИЦ УМНОЖЕНИЯ

Простая таблица умножения в PDF

Этот вариант таблицы умножения подойдет тем, кто бы хотел иметь возможность самому завершить дизайн. Например, можно сделать умножение на каждую цифру своим цветом. А можно поменять расположение столбиков, чтобы получился нестандартный размер листа.

К сожалению, шрифт в этот таблице поменять не получится, так как все цифры были переведены в кривые, зато ваша распечатанная таблица будет иметь точно такой вид, как на уменьшенной копии выше.

Скачать таблицу умножения в PDF (141 кб)

Таблица умножения на школьной доске картинкой

Если же вам нужно скачать готовый, завершенный и стильный вариант таблицы умножения, то этот шаблон для вас. Здесь и жирный шрифт, и стильный фон в виде школьной доски зеленого цвета.

Таблица умножения, как на тетрадке в клетку (Таблица Пифагора)

Учить таблицу наизусть удобнее всего по такой распечатке. Такое исполнение таблицы умножения мы знаем по тетрадям в клетку, для математики. Они были изображены на обратной стороне. Скачать таблицу Пифагора можно в DOC или PDF формате.

Шаблон таблицы умножения для маленьких детей

Шаблон выполнен в развлекательном стиле. Умножение на каждую цифру выполнено в столбик, и своим цветом. Под самой таблицей умножения танцуют забавные клоуны. Распечатать шаблон можно в формате А4.

Как умножать на 9: разбираем таблицу умножения на пальцах

Вы удивитесь, насколько это легко! Но чтобы умножать на пальцах на 9, нумеровать их нужно по-другому. Теперь мы меняем отсчет по порядку от 1 до 10, начиная с большого пальца левой руки:

Нумерация пальцев

Поворачиваем ладони также к себе. Большие пальцы смотрят в стороны. Кстати, если вам удобнее, то работайте с тыльной стороной. Только отсчет тогда будет от мизинца и до мизинца.

Разберем на примере 9 на 2

2*9

1. Наш указательный на левой руке имеет счет 2. Загибаем этот палец.
2. И теперь начинаем считать: по левую сторону от согнутого командира у нас только 1 палец; по правую сторону – 8.
3. В итоге просто складываем 1, что представляет собой 10, и 8. И получаем 18!

Есть еще более хитрый способ – числа не обязательно суммировать, их достаточно просто сложить в одно число.

Усложняем задачу — 7 умножить на 9

Умножаем 7 на 9

1. Цифру 7 означает безымянный палец правой руки. Будьте на этом этапе внимательны! Загибаем и начинаем считать.
2. До этого пальца у нас остались 6 незадействованных: большой палец левой руки, указательный палец левой руки, средний палец левой руки, безымянный палец левой руки, мизинец левой руки, мизинец правой руки.
3. Таким образом, цифра разряда десятков – это 6.
4. Все остальные свободные пальцы, которые находятся после седьмого пальца, а это средний палец правой руки, указательный палец правой руки, большой палец правой руки будут единицами.
5. Цифра разряда единиц – это 3.
6. Складываем их вместе. Вот мы и решили пример 7 на 9. Ответом будет число 63.

Пользуясь такими подсказками, ребенку будет нетрудно запомнить таблицу умножения. А на уроках он больше не будет нервничать, поскольку шпаргалка всегда будет «под рукой», а точнее на руках. Конечно, учить таблицу умножения нужно и считать в уме – это важная работа для мозга. Но куда лучше усваивается материал, если развить к нему интерес.

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

1. 55 единиц второго класса и 100 единиц первого класса;
2. 110 единиц второго класса и 5 единиц первого класса;
3. 7 единиц второго класса и 13 единиц первого класса.

Ответ:

1. 55 100;
2. 110 005;
3. 7 013.

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

• 10 единиц равны 1 десятку;
• 10 десятков равны 1 сотне;
• 10 сотен равны 1 тысяче;
• 10 тысяч равны 1 десятку тысяч;
• 10 десятков тысяч равны 1 сотне тысяч;
• 10 сотен тысяч равны 1 миллиону.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

Как рассуждаем:

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

• 11 627 — одиннадцать тысяч шестьсот двадцать семь.
• 31 502 — тридцать одна тысяча пятьсот два.

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

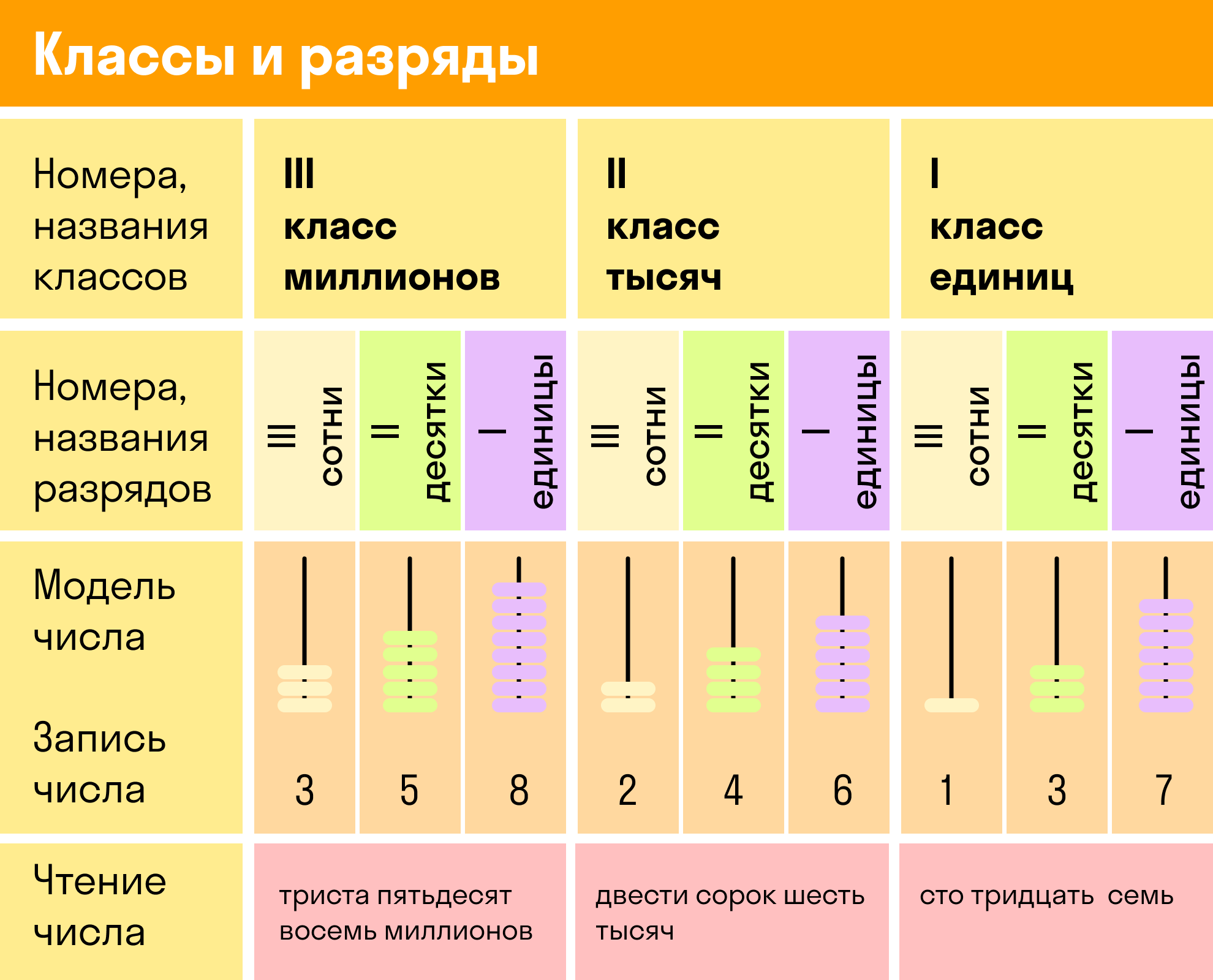
Таблица деления на 6

Таблица деления на 6

Если деление на 6 ребенку еще трудно дается, тогда пусть он попробует делить столбиком. Чем больше он будет заниматься с делением в столбик, тем быстрее малыш поймет алгоритм деления.

Таблица деления на 6:

0:6=0  (0 разделить на 6, получается 0)

6:6=1  (6 разделить на 6, получается 1)

12:6=2  (12 разделить на 6, получается 2)

18:6=3  (18 разделить на 6, получается 3)

24:6=4  (24 разделить на 6, получается 4)

30:6=5  (30 разделить на 6, получается 5)

36:6=6  (36 разделить на 6, получается 6)

42:6=7  (42 разделить на 6, получается 7)

48:6=8  (48 разделить на 6, получается 8)

54:6=9  (54 разделить на 6, получается 9)

60:6=10  (60 разделить на 6, получается 10)

Таблица умножения на 7 до 150

7 x 141 = 987(семь умножить на сто сорок один равно девятьсот восемьдесят семь)

7 x 142 = 994(семь умножить на сто сорок два равно девятьсот девяносто четыре)

7 x 143 = 1001(семь умножить на сто сорок три равно одна тысяча один)

7 x 144 = 1008(семь умножить на сто сорок четыре равно одна тысяча восемь)

7 x 145 = 1015(семь умножить на сто сорок пять равно одна тысяча пятнадцать)

7 x 146 = 1022(семь умножить на сто сорок шесть равно одна тысяча двадцать два)

7 x 147 = 1029(семь умножить на сто сорок семь равно одна тысяча двадцать девять)

7 x 148 = 1036(семь умножить на сто сорок восемь равно одна тысяча тридцать шесть)

7 x 149 = 1043(семь умножить на сто сорок девять равно одна тысяча сорок три)

7 x 150 = 1050(семь умножить на сто пятьдесят равно одна тысяча пятьдесят)

интернет проект BeginnerSchool.ru

Мы все знаем, что учить таблицу умножения необходимо. А необходимо потому, что зная назубок таблицу умножения/деления от 1 до 10, ребенок без труда освоит внетабличное умножение и деление. Но как же легче всего выучить таблицу умножения. Ответ неоднозначен, для каждого ребенка нужен индивидуальный подход. Но все же можно дать общие для всех советы.
Для начала надо объяснить ребенку, что такое умножение. Умножение связано с действием сложения. Объясните ребенку, что перемножаемые числа называются множителями, а полученное число называется произведением.

Итак, начинаем с умножения на 2:
Что такое 2 × 2, это 2 + 2 и равно 4. Положим две конфеты на одну тарелочку и еще две конфеты на другую. Если конфеты сосчитать все вместе получится четыре, то есть 2 конфеты умножить на 2 тарелочки, получится 4 конфеты: 2 × 2 = 4.

Теперь, чтобы проверить результат, разделите 4 конфеты обратно на две тарелки: 4 ÷ 2 = 2.

А как еще можно поровну разделить конфеты? Конечно же, по четырем тарелкам. Если на каждую тарелку положить по конфете:

• 4 ÷ 4 = 1
• 4 ÷ 1 = 4
•  проверим: 4 × 1 = 4.

Теперь добавим на каждую тарелочку еще по конфете. Считаем все конфеты, получаем 6, как получилось? Три конфеты умножили на две тарелочки: 3 × 2 = 3 + 3 = 2 + 2 + 2 = 6.

1. То есть три умножить на два это 2 раза по 3 или 3 раза по 2, и если взять три тарелочки по две конфеты, то все равно получится 6 конфет.
2. От перемены мест множителей произведение не меняется: 3 × 2 = 2 × 3 = 6.

Теперь деление: 6 ÷ 2 = 3, берем 6 конфет и раскладываем поровну на две тарелки, получаем на каждой по три конфеты. Также показываем деление шести конфет по трем тарелкам, получаем по две конфеты на каждой тарелке: 6 ÷ 3 = 2.

Таким образом, можно разобрать каждый пример умножения на 2, на 3 и так далее.
Когда ребенок уверенно будет решать такого рода примеры, приступайте к постепенному заучиванию таблицы умножения, сначала на 2, потом на 3 и так далее до 9.

• Объясните особенности умножения на 1 и на 10:
• При умножении любого числа на 1, в результате получите это же число:
• 1 × 1 = 1
•  1 × 2 = 2
•  1 × 3 = 3
•  1 × 99 = 99
• и так далее.
• При умножении любого числа на 10, в результате получим то же число, но с добавленным справа нулем: 10 × 3 = 30, один ноль, потому что в цифре 10 один ноль, а если умножать не на 10, а на 100, то получим справа два нуля: 100 × 3 = 300. И так далее с 1000, 10000…
• То есть для того, чтобы умножить число на 10, 100, 1000 и так далее (например 4 × 10), сначала вспоминаем правило умножения на 1, то есть пишем то же число (4) и дописываем к нему справа столько нулей, сколько во втором множителе (10), (4 × 10 = 40).
• Таблица умножения:
• Про особенности умножения на 9 мы писали в статье “Чудеса умножения“.
• О том как выучить таблицу умножения, читайте в статье “Как выучить таблицу умножения“.
• После того (или вместе с тем), как ребенок освоит таблицу умножения, знакомим его с таблицей Пифагора:
• В таблице Пифагора по вертикали (в первом столбце) и горизонтали (в первой строке) расположены числа от 1 до 10. На пересечении строк и столбцов располагаются произведения этих чисел:
• Проверить таблицу умножения можно следующим образом. Нарисуйте таблицу Пифагора, не заполняя произведения, заштрихуйте некоторые ячейки следующим образом:
• Теперь пусть ребенок самостоятельно заполнит заштрихованные клетки, должно получиться следующее:
• Теперь сами придумайте рисунок.
• Если вы хотите получать анонсы наших статей, подпишитесь на рассылку “Новости сайта”.