Умножение

Умножение многозначных чисел на многозначные

Умножение многозначных чисел на многозначные происходит таким же образом, как и умножение многозначных на однозначные. Каждая цифра многозначного числа умножается на каждую цифру другого многозначного числа. Единственное отличие заключается в том, что в конце образуется своего рода лесенка ответов, которые надо сложить. Рассмотрим несколько примеров, чтобы хорошо понять это.

Пример 1. Найти значение выражения 12 × 14

Записываем данное выражение в столбик — единицы под единицами, десятки десятками:

Теперь умножаем каждую цифру числа 12 на каждую цифру числа 14. Делать это надо по-очереди, начав с четвёрки. В результате таких действий мы приходим к умножению многозначного числа на однозначное, которое проходили ранее:

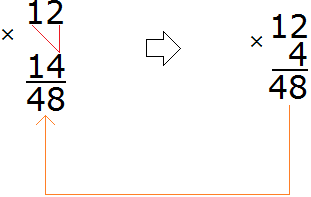
Умножив 12 на 4, мы получили число 48, которое записали таким образом, чтобы разряд единиц этого числа оказался под четверкой, на которую мы умножали число 12.

Теперь умножаем 12 на 1:

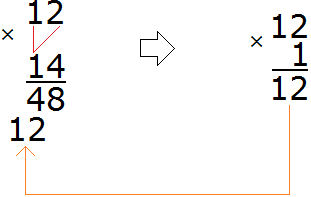
Умножив 12 на 1 мы получили число 12 и записали его таким образом, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножали число 12.

Мы получили лесенку ответов 48 и 12, которую надо сложить. Складываем и получаем ответ 168

В данном примере множитель 14 это четыре единицы и один десяток. Тогда умножение 12 на 14 можно понимать как увеличение числа 12 в четыре раза и в десять раз. Этим и объясняется появление лесенки в конце решения. Давайте посмотрим как это выглядит на каждом этапе:

Увеличим число 12 в четыре раза, получим число 48

Увеличим число 12 в десять раз, получим число 120. Записываем 120 так, чтобы можно было сложить единицы этого числа с единицами числа 48, а десятки числа 120 можно было сложить с десятками числа 48

Теперь сложим получившуюся лесенку ответов. Единицы сложим с единицами, десятки с десятками, сотни с сотнями. В результате образуется окончательный ответ:

Но чаще всего множитель не группируется с помощью разрядов, и умножение выполняют, умножая каждую цифру множимого на каждую цифру множителя.

Пример 2. Найти значение выражения 25 × 36

Записываем данное выражение в столбик

Умножаем каждую цифру числа 25 на каждую цифру числа 36.

Умножим 25 на 6:

Умножаем 25 на 3:

Теперь сложим получившуюся лесенку:

Получили ответ 900.

Рассмотрим большой и сложный пример на умножение: 12305 × 5641. Будем придерживаться ранее изученных правил.

Сначала записываем в столбик данное выражение

Теперь начинаем умножать. Число 12305 надо умножить на каждую цифру числа 5641.

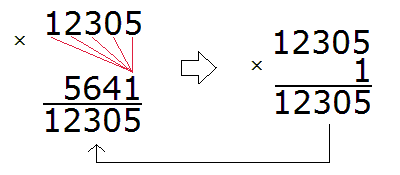
Умножив 12305 на 1, мы получили 12305 и записали это число так, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножили 12305.

Теперь умножаем 12305 на следующую цифру 4:

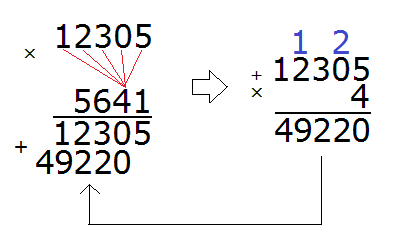Умножив 12305 на 4, мы получили 49220 и записали это число так, чтобы разряд единиц этого числа оказался под четверкой, на которую умножали 12305.

Умножаем 12305 на следующую цифру 6:

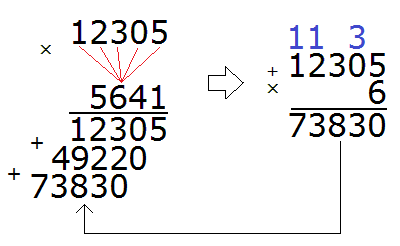
Умножив 12305 на 6, мы получили 73830 и записали это число так, чтобы разряд единиц этого числа оказался под шестёркой, на которую мы умножали 12305.

Теперь умножаем 12305 на последнюю цифру 5:

Умножив 12305 на 5, мы получили 61525 и записали это число так, чтобы разряд единиц этого числа оказался под пятёркой, на которую умножали 12305.

В результате мы получили большую лесенку, которую надо сложить. Складываем:

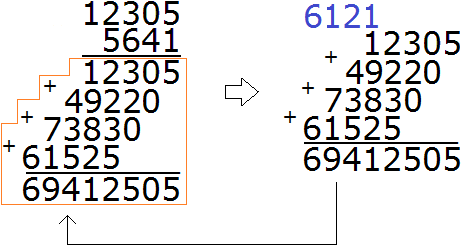
Получили окончательный ответ 69412505.

Если вы поняли этот пример, то можно сказать, что умножение больших чисел вы усвоили на отлично.

На этом урок по умножению можно завершить. Обязательно потренируйтесь, решив несколько примеров, которые даны ниже.

Важно отметить, что все эти стрелки и подробные решения, как на картинках в «боевых условиях» рисовать не принято. Нужно уметь сразу записывать ответы, выполняя в уме все вычисления

Исключением является то, если человек давно не занимался математикой или никогда ею не занимался. В таком случае можно рисовать для себя стрелки и другие вспомогательные схемы для хорошего усвоения материала.

Умножение на однозначное число

Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше. 

Возьмем пример 234 * 2:

1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.

2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.

3. Ответ запишем под чертой:

Производить действия необходимо в следующей последовательности:

На самом деле вам нужно только знать таблицу на 6

Умножение коммутативно. Если вы знаете 7 x 6 = 42, знайте, что 6 x 7 = 42, если 8 x 6 = 48, то  6 x 8 = 48, и если вы знаете 8 x 7 = 56, вы знаете, что 7 x 8 = 56, и вы будете уметь сократить количество фактов, оставшихся для изучения, до последних шести, упомянутых в начале. Вы можете даже обнаружить, что уже выучили некоторые из этих последних шести, просто прочитав эту статью.

6 х 6 = 36
7 х 6 = 42
8 х 6 = 48
7 х 7 = 49
8 х 7 = 56
8 х 8 = 64

Если вы прочитаете эту статью 2 или 3 раза, вы удивитесь, сколько вы сохраните. Вот и финальная сетка, по-настоящему разделенная и завоеванная!

Я разработал этот метод, когда писал свой блог по математике на GCSE, и мои дети обнаружили, что он им помог. Как вы думаете? Знаете ли вы какие-нибудь другие приемы, которые я должен включить в свой математический блог?

Игра 2

На игровом поле 100 квадратов с результатами умножения двух чисел, которые есть на игральных кубиках (от 1 до 6). Числа на поле повторяются!
Первый игрок бросает кубики и умножает выпавшие числа. Получившийся результат ищет на поле и рисует линию, соединяя любые две точки квадрата, внутри которого находится это число.
Второй игрок делает то же самое, и далее по очереди.
Когда игрок рисует линию, полностью закрывающую квадрат, он его закрашивает. Грани у квадрата могут быть нарисованы и соперником, главное — быть последним. После этого игрок, закрасивший квадрат, бросает кубики снова.
Побеждает игрок с наибольшим количеством закрашенных квадратов.

Скачать бесплатно таблицу умножения: PDF, PNG — 3mu.ru

Все знают, что таблица умножения — это азы всех математических знаний современного человека

Поэтому так важно, чтобы школьник ее выучил как можно раньше. Многие помнят, как на каждой тетрадке в клетку, с обратной стороны печаталась такая таблица

И не просто так, чем чаще к ней обращается ребенок, тем быстрее он научится считать большие примеры.

СПИСОК ТАБЛИЦ УМНОЖЕНИЯ

Простая таблица умножения в PDF

Этот вариант таблицы умножения подойдет тем, кто бы хотел иметь возможность самому завершить дизайн. Например, можно сделать умножение на каждую цифру своим цветом. А можно поменять расположение столбиков, чтобы получился нестандартный размер листа.

К сожалению, шрифт в этот таблице поменять не получится, так как все цифры были переведены в кривые, зато ваша распечатанная таблица будет иметь точно такой вид, как на уменьшенной копии выше.

Скачать таблицу умножения в PDF (141 кб)

Таблица умножения на школьной доске картинкой

Если же вам нужно скачать готовый, завершенный и стильный вариант таблицы умножения, то этот шаблон для вас. Здесь и жирный шрифт, и стильный фон в виде школьной доски зеленого цвета.

Таблица умножения, как на тетрадке в клетку (Таблица Пифагора)

Учить таблицу наизусть удобнее всего по такой распечатке. Такое исполнение таблицы умножения мы знаем по тетрадям в клетку, для математики. Они были изображены на обратной стороне. Скачать таблицу Пифагора можно в DOC или PDF формате.

Шаблон таблицы умножения для маленьких детей

Шаблон выполнен в развлекательном стиле. Умножение на каждую цифру выполнено в столбик, и своим цветом. Под самой таблицей умножения танцуют забавные клоуны. Распечатать шаблон можно в формате А4.

Как быстро и легко выучить таблицу умножения с ребёнком?

Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.

Совет в запоминании №1

Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.

Умножение – это сумма одинаковых слагаемых.

8 x 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8

Понимая смысл множителя, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.

Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.

Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32

Умножать можно с помощью рук Умножение на 9

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.

Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

Способ 2

Например, нужно выяснить сколько будет при счете 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Еще одни факты в обучении

Умножение ( х )- это коммутативная операция. Это означает, что вы можете изменить порядок чисел, и ответ будет таким же. Так например:

8 х 6 = 48 и
6 х 8 = 48

Хитрости в обучении таблицы умножения на 9

Все знают таблицу умножения на 10, но есть хитрость как узнать таблицу умножения на 9

Продолжая тему «разделяй и властвуй», мы можем покорить таблицу (х ) на девять и десять. Я полагаю, что каждый знает свою таблицу (х ) на девять, и большинство людей знают трюк, чтобы выучить таблицу умножения на девять.

Если вы не знаете трюка с таблицей (х ) на девять, вы можете выбрать из числа. Некоторые включают в себя очень простые вычисления в уме, другие заставляют вас использовать пальцы. Лучше всего выбрать трюк, который вам подходит. Просто погуглите «девятикратный трюк» и выберите свой любимый. Если вы потратите время, чтобы просмотреть один или два примера и сделать выбор, этот опят останется неизменным.

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041. 

Изменение произведения чисел при изменении его сомножителей

Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения, а также переместительный и сочетательный законы сложения.

Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.

Рассмотрим пример 18 ∙2. Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6.

Действительно:

18 ∙2 =3618 ∙6 =108.

Если мы увеличим 36 в 3 раза, то мы получим как раз 108.

По-другому и быть не может, и вот почему.

Первое произведение представляет собой сумму двух слагаемых:

18+18.

Второе произведение – это сумма шести таких же слагаемых:

18+18+18+18+18+18.

Если мы, воспользовавшись сочетательным законом умножения, сгруппируем эти слагаемые по 2, то получим следующее:

(18+18)+(18+18)+(18+18).

Как видите, у нас получилось 3 одинаковых слагаемых, каждый из которых равен первому произведению. А это значит, что полученное произведение состоит из трех, которые были даны изначально, то есть, в 3 раза больше начального. Что и требовалось доказать.

Для второго сомножителя справедливость этого свойства доказывается на основе переместительного закона умножения.

Если уменьшить один из сомножителей в несколько раз, произведение также уменьшится в это же число раз.

Если увеличить один из сомножителей в несколько раз, а второй в это же число раз уменьшить, то произведение при этом не поменяется.

Действительно, при увеличении одного из сомножителей , а при уменьшении другого сомножителя . Поэтому, если увеличить одно и одновременно уменьшить другое число, то эти изменения компенсируют друг друга, и произведение :

32 ∙8 =256,

Увеличим первый сомножитель в 4 раза, а второй во столько же раз уменьшим:

128 ∙2 =256.

Теперь уменьшим первый сомножитель произведения 32 ∙8 в 4 раза, а второй уменьшим в это же число раз:

8 ∙32 =256.

Как учить ребенка учиться

Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.

А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.

Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.

Умножение однозначных чисел

Умножение двух однозначных натуральных чисел a и b – это нахождения суммы b слагаемых, каждое из которых равно числу a, и при этом a и b являются натуральными числами.

Если a и b – числа, находящиеся в самом начале натурального ряда, то найти такую сумму особого труда не составляет: 1 ∙2=1+1=2. Но если взять числа, которые замыкают первый десяток, например, 8 и 9, то для вычисления 8 ∙9, а именно, суммы 8+8+8+8+8+8+8+8+8=72, то в этом случае вычисление результата потребует от нас определенного времени.

Для облегчения вычисления, были посчитаны результаты умножения всех однозначных чисел друг на друга, и сведены в специальные таблицы умножения.

Умножение однозначных чисел – это основа быстрого и точного вычисления произведений любых чисел, поэтому очень важно знать на память все таблицы умножения.

Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

Способ 2

Например, нужно умножить 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Совет № 3

Знание правил умножения упростит запоминание таблицы умножения:

При умножении любого числа на 1 получается то число, которое умножали.
Все результаты умножения на 10 начинаются с числа, которое мы умножаем, а заканчиваются на 0.
Все результаты умножения на 5 заканчиваются на 5 или 0: если умножали нечётное число – на 5, если чётное – на 0.
Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 на 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
При умножении на 9, запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.
Как быстро и легко выучить таблицу умножения

Умножение чисел, которые оканчиваются нулями

Если оба числа оканчиваются нулями, то нужно перемнóжить те цифры, которые нулями не являются, затем к полученному результату дописáть все нули из обоих чисел.

Например, умнóжим 20 на 30.

20 × 30

Видим, что оба числá содержат по нулю. Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 2 и 3. Два умножить на три будет шесть:

20 × 30 = 6

Теперь к полученному результату, то есть к числу 6 дописываем все нули из обоих чисел. В числе 20 один ноль, в числе 30 также один ноль. Итого два нуля. Дописываем два нуля к числу 6

20 × 30 = 600

Пример 2. Умножить 40 на 300

Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 4 и 3. Четыре умножить на три будет двенадцать:

40 × 300 = 12

Теперь к полученному результату, то есть к числу 12 дописываем все нули из обоих чисел. В числе 40 один ноль, в числе 300 — два нуля. Итого три нуля. Дописываем три нуля к числу 12

40 × 300 = 12000

Пример 3. Умножить 600 на 3000

Сначала перемнóжим те цифры, которые нулями не являются. Это цифры 6 и 3. Шесть умножить на три будет восемнадцать:

600 × 3000 = 18

Теперь к полученному результату, то есть к числу 18 дописываем все нули из обоих чисел. В числе 600 два нуля, в числе 3000 — три нуля. Итого пять нулей. Дописываем пять нулей к числу 18

600 × 3000 = 1800000

Вы здесь

Таблица умножения и деления

Файлы: 

Вложение	Размер
Таблица умножения и деления, картинка с пояснением	74.46 КБ
Таблица умножения и деления	105.44 КБ
Таблица умножения и деления без ответов	19.53 КБ

Чтобы скачать и рапсечатать таблицу умножения и деления, используйте ссылки выше или нажмите правую кнопку мышки над картинками ниже и выберите «сохранить картинку как».

Таблица умножения и деления без ответов.

Тип:

материал

• Все тесты. Проверка. Тренажер таблицы умножения.
  • Умножение на 1. Все тесты.
    • Умножение на 1 (ввести ответ
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (найти ответ
    • Умножение на 1 (найти ответ
  • Умножение на 2. Все тесты.
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (найти ответ
    • Умножение на 2 (найти ответ
  • Умножение на 3. Все тесты.
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (найти ответ
    • Умножение на 3 (найти ответ
  • Умножение на 4. Все тесты.
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (найти ответ
    • Умножение на 4 (найти ответ
  • Умножение на 5. Все тесты.
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (найти ответ
    • Умножение на 5 (найти ответ
  • Умножение на 6. Все тесты.
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (найти ответ
    • Умножение на 6 (найти ответ
  • Умножение на 7. Все тесты.
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (найти ответ
    • Умножение на 7 (найти ответ
  • Умножение на 8. Все тесты.
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (найти ответ
    • Умножение на 8 (найти ответ
  • Умножение на 9. Все тесты.
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (найти ответ
    • Умножение на 9 (найти ответ
  • Умножение на 10. Все тесты.
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (найти ответ
    • Умножение на 10 (найти ответ
  • Тест-тренажер онлайн! Таблица умножения
  • Тест-тренажер онлайн! Таблица умножения. 10 вопросов.
• Умножение
  • Умножение на 1
  • Умножение на 2
  • Умножение на 3
  • Умножение на 4
  • Умножение на 5
  • Умножение на 6
  • Умножение на 7
  • Умножение на 8
  • Умножение на 9
  • Умножение на 10
• Таблица умножения до 20 и до 100
• Таблица умножения и деления
• Умножение в столбик
• Еще
  • Таблица сложения
  • Линейка
  • Без ответов
  • Таблица кубов
  • Таблица степеней
  • Калькуляторы
    • Умножение
    • Найти неизвестный множитель
    • Деление
    • Сложение
    • Кубов
  • Шпаргалка

Умножение на 10, 100, 1000

Чтобы умножить любое число на 10,  100 или 1000, достаточно дописáть к множимому количество нулей из множителя.

Например, чтобы умножить 12 на 10, нужно к множимому 12 дописать в конце ноль из множителя 10. В результате получим ответ 120

Еще примеры:

12 × 100 = 1200 (к 12 дописали два нуля, поскольку в числе 100 два нуля)

12 × 1000 = 12000 (к 12 дописали три нуля, поскольку в числе 1000 три нуля)

15 × 100 = 1500 (к 15 дописали два нуля, поскольку в числе 100 два нуля)

320 × 100 = 32000 (к 320 дописали два нуля, поскольку в 100 два нуля)

Если нулём оканчивается не множитель, а множимое, то для получения ответа нужно дописать ноль после множителя.

Например, чтобы умножить 10 на 12, нужно в ответе записать множитель 12 и дописать в конце один ноль:

10 × 12 = 120

Алгоритм умножения в столбик

Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:

1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.

2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения

Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д

3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.

Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.

5. Складываем то, что нашли и получаем ответ.

Таблица умножения для детей: способы запоминания

Чтобы помочь ребенку быстро выучить таблицу умножения, нужно понимать сам процесс умножения.Для начала ребенок должен хорошо уметь считать и понимать, например, что к  2 яблокам прибавить ещё 2 яблока будет 4

Важно, чтобы малыш правильно произносил цифры и не путал их. Только тогда можно приступить к изучению таблицы Пифагора

Таблица Пифагора для детей скачать и распечатать

К занятиям родители должны приготовить различные одинаковые предметы: кружочки, квадратики, яблоки, груши и др. Последние лучше вырезать из картона. Затруднений при умножении на единицу у ребенка возникнуть не должно. Начнем с умножения на 2. Для этого следует разложить, например, картонные яблоки или другие предметы 4 ряда по 2 единицы. Предложите ребенку посчитать количество рядов и предметов. Объясните, что если умножить 2 ряда на 2 предмета, будет 4; 4 ряда на 2 предмета будет 8 и т. д. Когда ребенок освоит умножение на два, переходите к умножению на три. Здесь уже сделайте 3 ряда по 3 предмета.

Скачать таблицу умножения на 2

Как выучить таблицу умножения в игровой форме

Другой быстрый способ, который поможет выучить таблицу умножения, это изучение в игровой форме. Этот метод следует применять тогда, когда ребенок «вызубрил» таблицу и имеет некоторые пробелы.  Данный игровой метод представляет собой игру в фанты. Необходимо сделать заготовку карточек, на которых написать умножения на различные числа.

Принцип игры следующий: ребенку предлагаете взять любую карточку, к примеру 5×7, при правильном ответе карточку кладет к себе, если ответ неверный карточка кладется вниз колоды. Путем повторения одних и тех же примеров,  ребенок их легко запомнит и усвоит.

Если в семье два школьника, то это будет отличным вариантом изучения таблицы умножения. При этом у ребенка задействована не только механическая, но и зрительная память.

Чтобы работала не только механическая, но и визуальная память, Скачайте таблицу умножения (плакат), распечатайте и повесьте  на видное место. Приобрести можно и специальные магнитики с цифрами на холодильник. Ребенку не будет скучно  учить  одному. Вы на кухне готовите ужин, а малыш учит таблицу, передвигая правильно магнитики. В помощь ребенку сейчас имеется большой выбор различных товаров. Поэтому у родителей не должно возникнуть трудностей, при выборе таблице умножения.

Таблица умножения в стихах

Следующий прием, который поможет ребенку выучить таблицу умножения, мнемонический. Суть его в том, что ребенок заучивает рифмованные слова или ассоциации.

Таблица умножения на 3 в стихах

Изучение таблицы умножения требует усидчивости и терпения от школьника, но некоторые способы запоминания таблицы умножения облегчат запоминание, и сделают его веселым и быстрым.

Например, вот так легко запомнить таблицу умножения на 9.

Распечатать таблицу умножения на 9

Эффективный способ запоминания умножения на 9

Однозначные и многозначные числа

Для начала введём два новых понятия: однознáчные и многознáчные числа.

Однознáчным называется число, которое состоит из одной цифры. Например, следующие числа являются однознáчными:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Слово «однознáчные» говорит само за себя. Однознáчное — значит состоит из одного знака (цифру иногда называют знáком).

Многознáчным называется число, которое состоит из двух и более цифр. Например, следующие цифры являются многознáчными:

10, 11, 15, 255, 350, 1000, 12500

Многознáчных чисел бесконечно много. Их не сосчитать. Кроме того, они подразделяются на следующие виды:

• двузнáчные, которые состоят из двух цифр (например, 25);
• трёхзнáчные, которые состоят из трёх цифр (например, 563);
• четырёхзнáчные, которые состоят из четырёх цифр (например, 1400)

и так далее, в зависимости от того сколько цифр в числе.

Тренажер по таблице умножения и деления

Бесценный богатый тренажер!
В книге вы найдете:

•  страницы интересных результативных упражнений;
• разнообразные задания;
• творческий подход;
• нестандартные приемы;
• задания разного уровня сложности;
• различные шифровки;
• игры и раскраски.
• Ваш ребенок получит:

легкое и без нервов запоминание таблицы умножения;
развитие внимания и мышления;
улучшение в целом математических способностей;
огромное количество интересных и полезных заданий.
Книга может быть использована как для индивидуальной работы, так и работы в классе.
Скучно точно не будет!

Тренажер удобен для распечатывания!

Умножение многозначного числа на однозначное

Допустим, нам нужно умножить 985 на 4. Умножить 985 на 4 – это сложить4 раза число 985, то есть, 985+985+985+985. Мы можем представить каждое из слагаемых 985 в виде суммы его разрядных слагаемых, а именно: 900+80+5. Получится такое выражение:

900+80+5+900+80+5+900+80+5+900+80+5.

Воспользуемся законами сложения и сгруппируем одинаковые слагаемые этого выражения вместе:

900+900+900+900+80+80+80+80+5+5+5+5,

(900+900+900+900)+(80+80+80+80)+(5+5+5+5).

Суммы в скобках мы можем заменить на произведение одинаковых слагаемых и числа этих слагаемых в каждых скобках:

900 ∙4+80 ∙4+5 ∙4.

Таким образом, чтобы умножить многозначное число на однозначное, достаточно умножить это однозначное число на количество единиц в каждом разряде многозначного числа, и сложить полученные результаты.

Умножение в столбик многозначного числа на однозначное

Удобно и быстро умножить многозначное число на однозначное, и при этом не запутаться в расчете помогает запись вычисления в столбик.

Для этого пишем множимое 985, и под цифрой его разряда единиц записываем множитель 4. Проводим под множителем горизонтальную черту, ставим между сомножителями знак умножения (точку или косой крест), и получаем такую запись:

4 раза по 5 единиц – это будет 20 единиц, то есть, 2 десятка и простых единиц. Поэтому, пишем под чертой в разряде единиц , а 2 десятка запоминаем или записываем маленькую цифру 2 над разрядом десятков множимого 985:

4 раза по 8 десятков – это 32 десятка. Прибавим к ним 2 десятка, которые получились после умножения однозначного числа на единицы, получим 32 десятка, то есть, 3 сотни и 2 десятка. Цифру 2 пишем под чертой в разряде десятков, а над разрядом сотен множимого 975 (в уме) ставим маленькую цифру 3:

4 раза по 9 сотен – это 36 сотен. Прибавим к ним 3 сотни, которые держим в уме, получаем 39 сотен, или 3 тысячи и 9 сотен. Значит, пишем под горизонтальной чертой в разряде сотен цифру 9 и, поскольку в множимом 985 нет ни одной тысячи, то сразу запишем в результате под чертой цифру 3 в разряде тысяч:

Распределительный закон умножения (умножение суммы на число)

Когда мы рассматривали умножение многозначного и однозначного чисел, мы раскладывали число 975 на его разрядные слагаемые (900+70+5), а потом умножали на 4 отдельно каждое это слагаемое. Аналогично можно поступать при умножении числа на любую сумму.

Например, найдем произведение суммы 5+2+4+9 и числа 3. Это означает, что нужно найти такую сумму:

(5+2+4+9)+(5+2+4+9)+ (5+2+4+9).

Все эти слагаемые представляют собой одну сумму чисел, сгруппированных в определенные группы. Запишем их без скобок:

5+2+4+9+5+2+4+9+5+2+4+9,

а затем, используя переместительный и сочетательный законы сложения, сгруппируем одинаковые слагаемые:

(5+5+5)+(2+2+2)+(4+4+4)+(9+9+9).

Основываясь на определении действия умножение, так как мы имеем в каждых скобках одинаковые слагаемые, переписываем это выражение следующим образом:

5 ∙3+2 ∙3+4 ∙3+9 ∙3.

Распределительный закон умножения: для умножения суммы на любое число, необходимо каждое слагаемое этой суммы умножить на данное число, а затем сложить полученные произведения.Согласно переместительному закону умножения, это свойство справедливо и при умножении числа на сумму.Для умножения числа на сумму, необходимо умножить данное число на каждое слагаемое этой суммы, а результаты полученных произведения сложить.(a+b+c+d)∙z =z∙(a+b+c+d) =a ∙z+b ∙z+c ∙z+d ∙z.

Название распределительный происходит от того, что действие умножения на сумму распределяется между каждым из слагаемых этой суммы.

Вместо заключения

Уделяйте математике достаточно внимания уже с начальной школы. Этот предмет не только тренируем мозг в устном счете, но и умении логически мыслить, развивать смекалку. Постепенно привыкая к выполнению дополнительных и основных заданий, ребенок учится учиться, выполнять требования учителя, грамотно планировать свое время, распределять время для учебы и досуга.

Математические задания для третьеклассников моно составлять самостоятельно по приведенным нами аналогии, это не составит особого труда. Зато ваш ученик сможет больше тренироваться в математике, выполнять задания на каникулах и выходных, а также заниматься дополнительно после школы.

Как выучить таблицу умножения за 5 минут — 8 лайфхаков

1. Используйте стишки и песни. Ну а если ребенок лучше анализирует данные глазами, обязательно купите ему плакат с таблицей и повесьте над письменным столом;
2. Разберите с ребенком умножение на физическом уровне. Сделать это можно хоть с помощью конфет, хоть с помощью счетных палочек. Можно и немного почертить: покажите, что 2*4 эквивалентно двум рядам из четырех клеточек в его тетради и так далее;
3. Изучайте таблицу постепенно, не перегружая мозг школьника. Например, разбейте изучение по разным группам чисел. В один день разберитесь с умножением на два, в другой — на три и по такому же принципу дальше;
4. Задавайте вопросы. Например, покажите табличку ребенку и спросите: как думаешь, почему здесь так расположены цифры?» Ребенок посоображает и выдаст предположение. А вы его поправьте где нужно и предложите легкий способ запомнить нахождение чисел.
5. Наблюдайте за эмоциональным состоянием ребенка. Ребенок доволен — отлично, продолжаем дальше.Капризничает — он устал, дайте отдых. Не давите на него, не упрекайте за ошибки и не пытайтесь сравнивать его успехи с чужими вне игровой формы;
6. Уделяйте достаточно времени и внимания повторению. Если будете заниматься с ребенком по 5 — 10 минут в день — этого в первое время достаточно. Затем увеличьте время до 10 — 15 минут. И наконец сделайте 3-4 занятия по 15 минут ежедневно, пока вся таблица не будет выучена.
7. Следите за скоростью, с которой школьник вычисляет. Если он немного медлит в самом начале изучения таблицы умножения, это вполне естественное. Если он продолжает брать паузы перед ответами, когда материал уже полностью пройден, мягко просите его отвечать скорее.