Решение простых линейных уравнений

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

• 2 — это первое слагаемое,
• 5 — второе слагаемое,
• 7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

Свойства сложения Переместительное свойство сложения От перестановки мест слагаемых сумма не меняется. a + b = b + a Сочетательное свойство сложения Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа. (a + b) + c = a + (b + c) Свойство нуля при сложении Если к числу прибавить нуль, получится само число. a + 0 = 0 + a = a

На заметку!
При сложении нескольких чисел, их можно объединять в группы и переставлять в любом порядке. Например: a + b + с = (a + b) + c = a + (b + c).

Сложение и умножение вероятностей

Немного теории:

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂,…, A_n образуют полную группу несовместных событий, то справедливо равенство: 

P(A1) + P(A2) + … + P(An) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

Как рассуждаем:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Значения сложноподчиненных предложений

В русском языке есть две группы придаточных предложений — именные и обстоятельственные. Они отличаются друг от друга по смыслу и характеру подчинительной связи с главным предложением. Рассмотрим каждую группу сложноподчиненных предложений на примерах.

Именные придаточные предложения

Эти предложения играют роль дополнений и определений по своему значению и связи с главным предложением. Их принято разделять на две подгруппы: определительные и изъяснительные.

Определительные придаточные предложения описывают существительное или местоимение в главном предложении. К ним можно задать вопрос «какой?»:

Хорош тот человек (какой?), который трудится над собой, а не других оценивает.

К главному предложению определительное придаточное присоединяется союзами и союзными словами который, какой, чей, кто, куда, будто и т. д.

Изъяснительные придаточные предложения поясняют глаголы и другие слова, которые означают речь, мысли и чувства. К таким придаточным можно задать вопросы косвенных падежей:

Отец завещал (что?), чтобы мы не забывали родину.

С главным предложением изъяснительное придаточное соединено подчинительной связью — союзами и союзными словами что, как, чтобы, где, откуда, зачем и т. д.

Эмпирическая база исследования: примеры

Можно долго читать характеристики эмпирической базы и так и не разобраться, что это такое на самом деле. Поэтому мы собрали реальные примеры описания, которые можно встретить в курсовых, дипломах и диссертациях. Изучайте образцы и используйте их в качестве шаблона для своего исследования.

Примеры описания эмпирической базы исследования в курсовых

Курсовая работа по социологии

Тема: «Российские женщины-политики в социальных медиа: анализ сетевых аккаунтов»

Аккаунты отбирались по следующему принципу:

Посты на страничках должны публиковаться не реже раза в неделю, в противном случае аккаунт будет считаться заброшенным.

В выборку попадают аккаунты политиков разных рангов:

• высший эшелон власти — министры;
• депутаты, пресс-секретари; 
• местные политики.

Для каждой группы было отобрано 2-3 наиболее популярных представителя. Степень их известности и популярности оценена при помощи статистики их цитирования в СМИ. Также учитывалось то, насколько популярны их аккаунты (сколько у них фолловеров).

Курсовая работа по психологии

Тема: «Психологический анализ особенностей формирования искусственного билингвизма у аутичных детей»

Эмпирическая база исследования: В исследовании приняли участие две группы детей (экспериментальная и контрольная), насчитывающие 15 испытуемых, в возрасте 10-11 лет, проживающих на территории Москвы и Московской области, с диагностированным расстройством аутичного спектра, не отягощённым умственной отсталостью.

Примеры описания эмпирической базы исследования в дипломных

Дипломная работа по финансовому праву

Тема: «Особенности правового регулирования деятельности иностранных юридических лиц на российском рынке ценных бумаг»

Эмпирическая база исследования: Фактологической основой работы явились статистические сведения Госкомстата России, Минфина России, ФСФР России, Банка России, официальные материалы МНС России, а также другие официальные источники.

Дипломная работа по медицине

Тема: «Профессиональный онтогенез: медико-социологические и психолого-этические проблемы врачебной деятельности»

Эмпирическая база исследования: Исследования проводилось на базе Волгоградского государственного медицинского университета путём анкетирования. В исследовании приняли участие студенты младших и старших курсов лечебного и педиатрического факультетов, а также врачи ЛПУ и Центра санэпиднадзора г. Волгограда и г. Волжского.

Пример описания эмпирической базы исследования в диссертации

Диссертация по праву

Тема: «Право и корпоративные нормы»

Эмпирическая база исследования: Эмпирической базой исследования является обобщение практической деятельности ряда организаций, как местного, так и межрегионального масштаба, в основу которого было положено изучение и детальный анализ корпоративных актов указанных структур.

Все образцы описания эмпирической базы исследования в курсовых работах, дипломах и диссертациях вы можете скачать в формате Word.

Надеемся, теперь вы сможете уверенно описать эмпирическую базу своего учебного исследования и с лёгкостью защитите его перед комиссией. А если не хватает времени оформлять реферат, курсовую или дипломную самостоятельно — доверьте это нашему студенческому сервису.

Знаки препинания в сложноподчиненных предложениях

Если придаточная часть сложноподчинительного предложения стоит перед или до главной, принято ставить запятую между ними. Если же она стоит в середине, зависимое предложение нужно обособлять с обеих сторон.

Примеры:

• Когда грузовик свернул к деревне, озеро осталось позади.

• Озеро остались позади, когда грузовик свернул к деревне.

• Сейчас, когда грузовик свернул к деревне, озеро осталось позади.

Если перед составными союзами есть слова лишь, только, еще и, прежде всего, именно, очевидно, вероятно или частицы не и ни, для таких союзов характерно деление. В таком случае перед что нужно ставить запятую:

Он заболел лишь потому, что ходил без шарфа зимой.

Если изъяснительные и условные (с союзом ли) придаточные стоят перед главным предложением и выделены интонацией, их разделяют тире:

Кто хочет — тот добьется.

Иногда перед подчинительные союзом ставят двоеточие. Например, если в части перед ним есть предупреждение о том, что дальше будет разъяснение:

Отец понял то, что ему нужно было понять: что они говорили о нем.

То же самое может быть и в бессоюзном предложении

И тогда он понял: все эти разговоры бесполезны.

Карточка 2

Сосчитай, записывая примеры в столбик.

32+49	37-16
46+24	70-48
83+8	53-38
38+32	45-8

Сосчитай, записывая примеры в столбик.

80-67	45+14
93-48	38+47
59-42	75+8
36-9	68+27

Сосчитай, записывая примеры в столбик.

46+37	80-38
22+58	93-56
59+9	75-9
64+27	87-32

Карточка 7

В летний лагерь приехали дети на двух автобусах. В первом автобусе было 46 детей, а во втором — на 8 детей меньше. Сколько всего детей приехало в школьный лагерь?

3∙7	2∙9	5∙3	9∙0
20:4	70:10	8∙10	32:4
27:3	21:7	7∙4	8∙3

c∙4=12

6∙c=18

27:c=3

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

2∙7	5∙9	8∙3	8∙4
25:5	8∙10	7∙0	60:6
36:4	16:4	21:7	15:3

c∙3=12

8∙c=24

25:c=5

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

70-(7∙3)+(8∙4)

Найди значение выражения, решая по действиям.

64-(27+14)+(6∙4)

Найди значение выражения, решая по действиям.

60-(8∙3)+(4∙7)

Найди значение выражения, решая по действиям.

38+(6∙3)-(4∙7)

Карточка 20

На зиму мама закрыла 4 банки вишнёвого варенья, а малинового — в 3 раза больше. Сколько банок малинового варенья закрыла мама? Сколько всего банок закрыла мама на зиму?

Карточка 21

В первый день маляр покрасил 5 скамеек, а во второй — в 4 раза больше. Сколько скамеек покрасил маляр во второй день? Сколько всего скамеек покрасил маляр за два дня?

Карточка 22

Пятачок за неделю съел 3 баночки мёда, в Винни-Пух — в 3 раза больше. Сколько баночек мёда съел Винни-Пух? Сколько баночек мёда они съели вместе?

Карточка 23

Перед домом посадили 4 ели, а берёз — в 3 раза больше. Сколько посадили берёз? Сколько всего деревьев посадили перед домом?

Карточка 24

Денис нарисовал 16 флажков, а Дима — в 4 раза меньше. Сколько флажков нарисовал Дима? Сколько всего флажков нарисовали мальчики?

Карточка 25

Алёна придумала 12 загадок, а Максим — в 2 раза меньше. Сколько загадок придумал Максим? Сколько всего загадок придумали оба мальчика?

Карточка 26

Мастер за день изготовил 24 детали, а его ученик — в 3 раза меньше. Сколько деталей изготовил ученик? Сколько всего деталей они изготовили вместе?

Карточка 28

На первом острове живёт 32 индейца, а на втором — в 4 раза меньше. Сколько индейцев живёт на втором острове? Сколько всего индейцев на двух островах?

Карточка 29

В куске было 54 метра ткани. Из этой ткани сшили 8 курток, расходуя по 3 метра на каждую. Сколько метров ткани осталось в куске?

В театре ученики первого класса заняли в партере 2 ряда по 9 мест и еще 13 мест в амфитеатре. Сколько всего мест заняли ученики первого класса?

Актовый зал освещает 6 люстр по 8 лампочек в каждой, да еще 7 лам­почек над сценой. Сколько всего лампочек освещает актовый зал?

К празднику купили 4 набора шариков по 10 штук в каждом наборе. Лопнули 12 шариков. Сколько шариков осталось на празднике?

В 3 одинаковых наборах 18 карандашей. Сколько карандашей будет в 7 таких наборах?

Начерти таблицу и реши задачу.

Для изготовления 5 одинаковых конструкторов потребовалось 35 деталей. Сколько деталей нужно для изготовления 8 таких конструкторов?

Начерти таблицу и реши задачу.

Крупу разложили на 6 одинаковых упаковок общей массой 12 кг. Сколько упаковок получится из 20 кг?

Начерти таблицу и реши задачу.

В 3 банки для засолки разложили 12 кг помидоров. Сколько банок потребуется для засолки 32 кг помидоров?

Начерти таблицу и реши задачу.

На 32р. купили 4 тетради. Сколько тетрадей можно купить на 56 рублей? на 16 рублей?

Начерти таблицу и реши задачу.

В 2 ведра помещается 16 кг картофеля. Сколько вёдер нужно, чтобы разложить 24 кг картофеля?

Начерти таблицу и реши задачу.

В 4 наборах 32 листа цветной бумаги. Сколько наборов составляют 72 листа бумаги?

Начерти таблицу и реши задачу.

• Начерти прямоугольник со сторонами 8 см и 4 см. Найди его площадь и периметр.
• Сравни:

12 смc1см2мм	7 мc74 дм	9 ммc1 см
14 смc1дм4см	8см7ммc90 мм	100 смc1 м

• Начерти прямоугольник со сторонами 5 см и 4 см. Найди его площадь и периметр.
• Сравни:

14 смc1см4мм	9 мc94 дм	9 ммc1 см
18 смc1дм8см	6см7ммc70 мм	10 смc1 дм

Расставь знаки «+», «-», «·», «: » так, чтобы равенства стали верными.

26*6*7=13	2*2*4=0
7*9*2=18	8*9*2=70
9*9*2=20	8*4*2=30
9*2*2=16	40*5*7=56

Из 12 м ткани портной сшил 6 одинаковых костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?

Начерти таблицу и реши задачу.

В огороде собрали 24 кг моркови, редиса — в 4 раза меньше, чем моркови, а чеснока — в 5 раз больше, чем редиса. Сколько килограммов чеснока собрали?

Из 15 м тюля сшили 5 одинаковых занавесок. Сколько таких занавесок можно сшить из 21 м тюля? Сколько понадобится тюля, чтобы сшить 9 таких занавесок?

Начерти таблицу и реши задачу.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2- 4ac = 4n2 — 4ac = 4(n2- ac) и подставим в формулу корней:

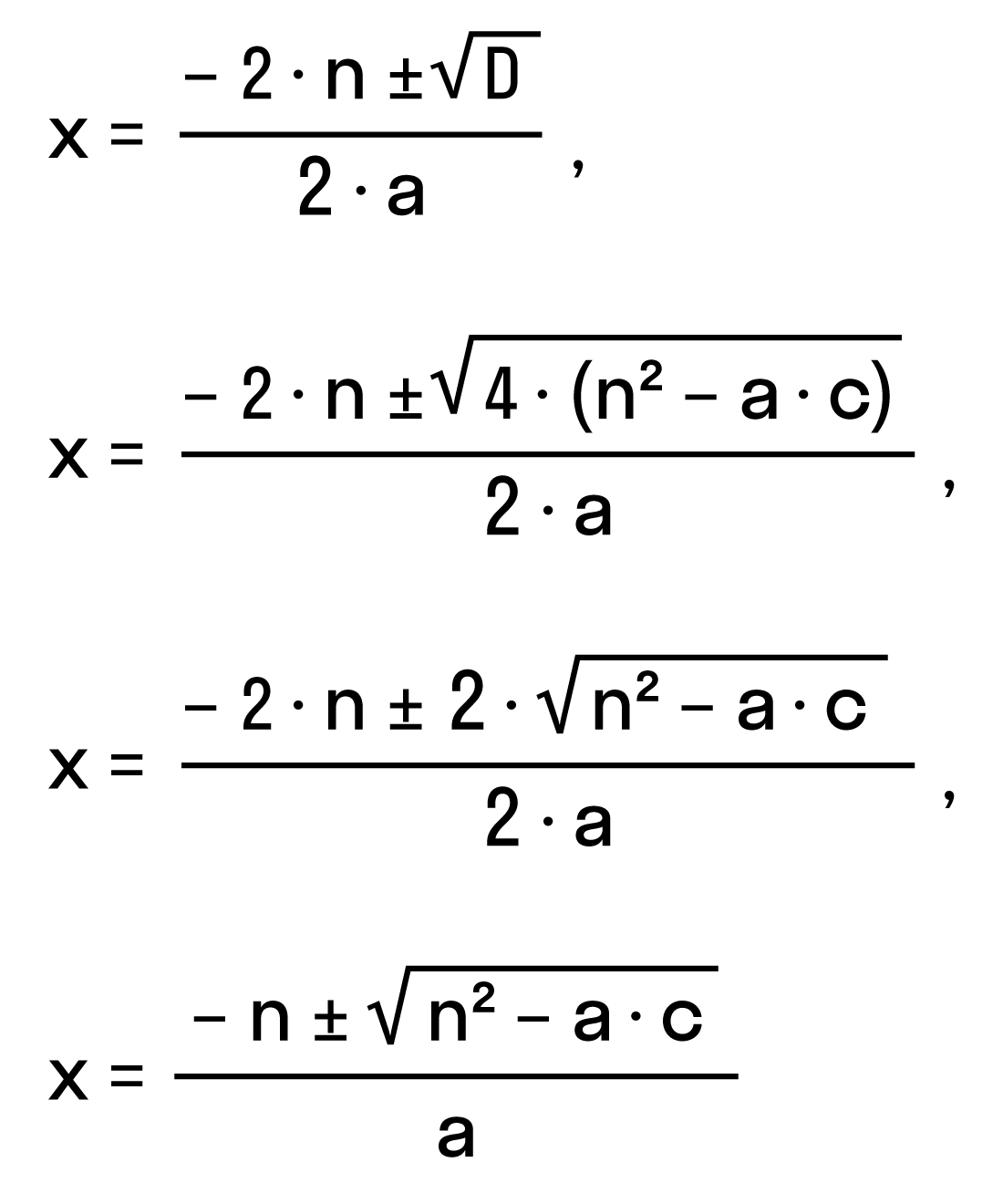
Для удобства вычислений обозначим выражение n2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n2- ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n2- ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11×2 — 4 x — 6 = 0, чем 1100×2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100×2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12×2- 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2×2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2×2- 3x + 7 = 0 перейти к решению 2×2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3×2- 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ: 16/10 = 1,6.

Пример 2. Перевести 37/1000 в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Пифагора: x2 − 6x + 8 = 0.

Как решаем:

1. Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2. Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

   Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

   Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

3. Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Сложноподчиненное предложение

Сложноподчиненное предложение (СПП) — это вид сложного предложения, в составе которого одно простое предложение по смыслу и интонации подчиняется другому. В этом случае зависимое предложение называется придаточным, а независимое — главным.

Пример сложноподчиненного предложения:

Мне было сложно понять, как ей удалось так быстро привыкнуть к новому городу.

Виды связи в сложноподчиненном предложении

Обычно части СПП в русском языке связаны друг с другом подчинительными союзами, например:

Я только-только закончил картину, когда солнце уже готовилось потухнуть.

Бывают сложные предложения, в которых придаточное с главным связаны только по смыслу и разделены знаком препинания, но между ними все еще можно вставить подчинительный союз. Такие предложения называют бессоюзными.

Пример:

На меня нахлынуло осознание: (что) все это время меня обманывали

Значения придаточных предложений в СПП

Придаточные предложения в составе сложных делятся на группы, а далее — на подгруппы по смыслу и виду связи с главным.

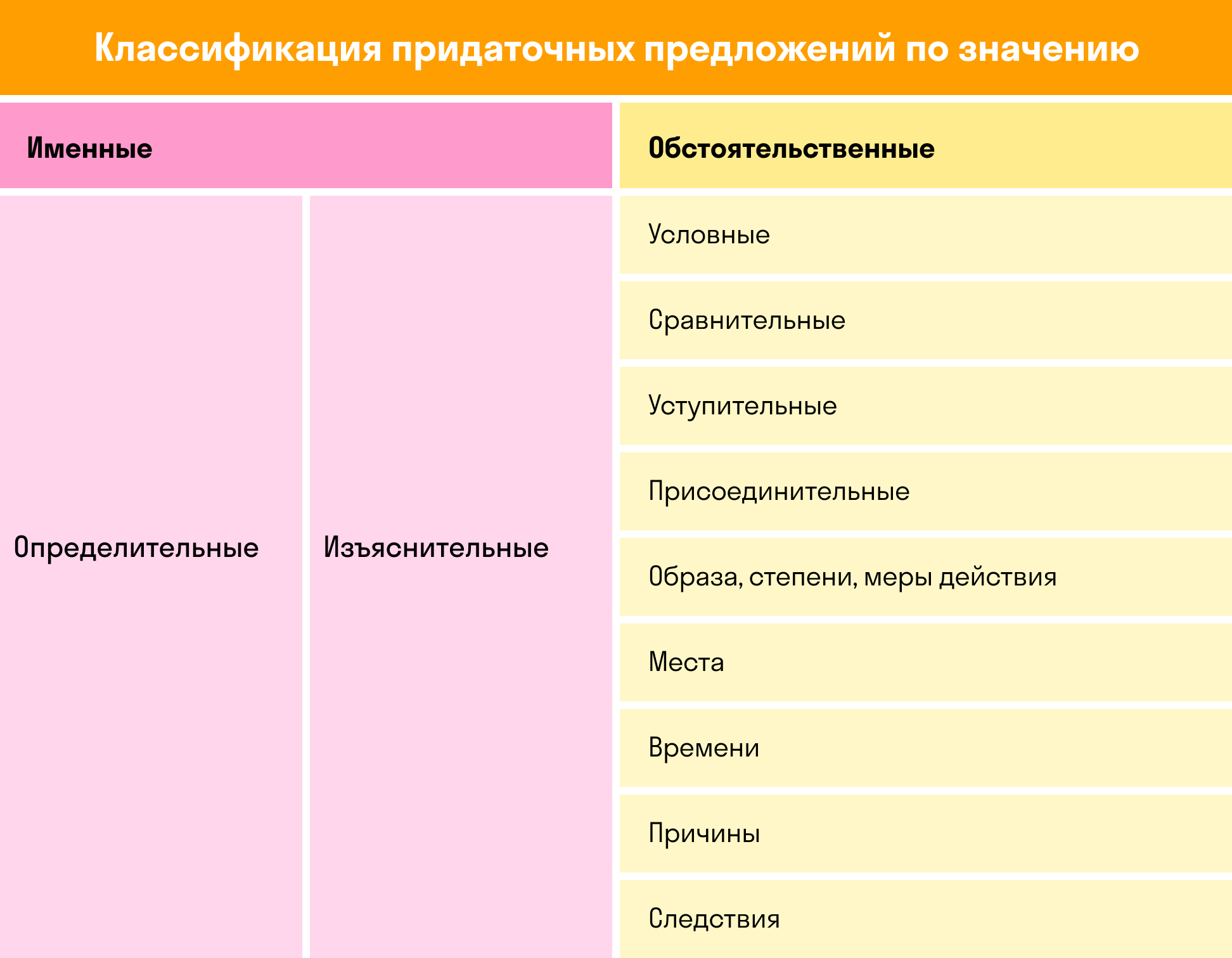
Подробнее о различиях между придаточными в сложном предложении с примерами можно прочесть в этой статье.

Типы подчинения в сложноподчиненном предложении

Иногда в сложноподчиненном предложении не одно, а два и более придаточных. Такой вид сложных предложений называют многочленными. Для них справедливы разные типы подчинения.

Подробнее эту тему мы уже разбирали в статье о сложноподчиненных предложениях.

Знаки препинания в сложноподчиненных предложениях

Между главной и придаточной частями сложного предложения принято ставить запятую. Если одна часть стоит в середине другой, выделять запятой ее нужно с обеих сторон:

• Когда мы вернулись в город, все горести остались за плечами.

• Сейчас, когда мы вернулись в город, все горести остались за плечами.

Если предложения со словами лишь, только, еще и, прежде всего, именно, очевидно, вероятно связаны составным союзом, он разделяется. Тогда перед словом что нужно ставить запятую:

Он согласился лишь потому, что я хорошо попросила.

Если мы выделяем интонацией изъявительные или условные придаточные и ставим их перед главным предложением, между ними ставится тире:

Кто желает — тот получит.

Если по главному предложению понятно, что придаточное его пояснит, нужно ставить двоеточие. То же правило относится и к бессоюзным сложным предложениям:

Он вдруг осознал: дальше не стоит и пытаться.

Сочинение №2

Какого героя литературного произведения или фильма вы бы могли назвать родственной душой?

Есть ли будущее у мира, в котором нет места искусству? На мой взгляд, это приведёт к деградации и вырождению человечества. Именно произведения искусства делают нас более гуманными, милосердными, учат нас сопереживать другим людям. Например, книги называют «детьми разума», потому что они действительно возвышают человека и очищают его душу. Особенно приятно читать литературное произведение, на героя которого хочется равняться. Каких персонажей я могла бы назвать родственной душой?

В романе-эпопее Л.Н. Толстого «Война и мир» одна из главных героинь – Марья Болконская, честная и душевная девушка, которая восхищает своей природной чистотой и естественностью

Княжна Марья не отличается внешней красотой, скорее, наоборот, автор постоянно акцентирует внимание на её недостатках. Лицо девушки было «некрасивым и болезненным», отец не раз называет её «дурной» или «неловкой», а Анатоль Курагин отзывается о ней следующим образом: «Бедняга! Чертовски дурна!» Почему же эта героиня вызывает у читателей такую симпатию? У княжны Марьи большие, лучистые глаза, которые, как известно, являются зеркалом человеческой души

Действительно, эта робкая девушка обладает богатым внутренним миром, она всегда доброжелательна, искренне переживает за своих близких и умеет по-настоящему любить. Марья Болконская религиозна, живёт по христианским заповедям, согласно которым все люди равны и никому не следует желать зла. Героиня Толстого помогает «божьим людям», даёт образок брату, провожая его на войну, и отличается поразительным смирением и кротостью. Я думаю, что княжна Марья – идеал женщины, она заботлива и милосердна.

Ещё одной родственной душой я бы назвала заглавную героиню романа Ш. Бронте «Джен Эйр». Так же, как и княжна Марья, Джен некрасива и на первый взгляд кажется абсолютно посредственной и ничем не примечательной девушкой. Однако на самом деле героиня Бронте оказывается сильной, решительной личностью, всегда готовой постоять за себя и свои права. Её независимость, сила воли и чувство собственного достоинства не могут не вызывать восхищения. С детства Джен приходилось противостоять грубой и властной тёте, а затем выживать в тяжёлых условиях пансиона для сирот. Героиня преодолевает все препятствия и с честью выдерживает выпавшие на её долю испытания. При этом она сохраняет лучшие человеческие качества: способность к сочувствию, кристальную честность, искренность и бесстрашие. Так, она, не опасаясь за собственную жизнь, проводит последние минуты рядом с умирающей от чахотки подруги. Джен – достаточно гордая девушка, но эта гордость не имеет ничего общего с гордыней или эгоизмом. Она возвращается к любимому человеку, когда ему требуется её помощь и поддержка, заботится о нём до конца своих дней.

Действительно, герои художественных произведений могут стать для читателя лучшими друзьями и родственными душами. Сила духа, целеустремлённость, милосердие и внутренняя красота – вот те качества, которые позволяют мне назвать героинь Л.Н. Толстого и Ш. Бронте примерами для подражания. Конечно, у каждого читателя может появиться свой идеал. Те люди, которые ничего не читают, многое упускают и лишают себя эстетического наслаждения.

Добавить комментарий