Деление многозначных чисел столбиком на двузначное, трехзначное число в 3,4 классе: как объяснить ребенку + топ-10 примеров

Деление целых чисел

Между умножением и делением натуральных чисел существует связь. Это связано с тем, что при делении можно найти частное, которое при обратном действии будет считаться множителем. Иначе можно записать, что деление целых чисел служит нахождением одного из целых множителей.

Отсюда делаем вывод, что произведение целых чисел a и b с частным, равным с, можно представить обратным действием деления с на b  с частным равным а. Если произведение чисел 5 и -7 равна -35, отсюда имеем, что частное (−35)5 равняется -7, а (−35)(−7) с результатом 5.

Частное от деления считается целым тогда, когда получается результат без остатка, то есть целое число a должно делиться на число b с целым частным в результате.

Деление в столбик двузначных, трехзначных, многозначных чисел, чисел с нулями

Не нужно пугаться сразу, что процесс деления не простой, поэтому вы не освоите его. Освоите! В математике следует соблюдать четкие правила, тогда у вас все получится. Алгоритм деления лучше учить на конкретных примерах, ниже будет представлено множество примеров.

Пример деления на трехзначный делитель

Все они выполняются по схеме:

1. Вначале записывается делимое, рядом ставится значок разделить: Ι—, и над чертой пишется делитель (число, на которое делят делимое).
2. Потом необходимо выделить часть делимого для осуществления деления, если это необходимо в данном случае.
3. Далее придется выполнять умножение для того, чтобы определить, сколько раз взять делитель, чтобы получилась выделенная часть делимого. Причем число не должно быть больше 9-ти.
4. Выполняете умножение делителя, записываете результат под делимым, а число ≤ 9-ти записываете под черту знака: Ι– разделить.
5. Из выбранной части делимого вычитаете результат, записываете его под подчеркиванием, сносите следующую цифру делимого, повторяйте опять процесс умножения, пока не разделите число на число.

Рассмотрим деление в столбик на простом примере:

Если такие двухзначные числа, как 16, 28 можно разделить в уме на 2 или 4 (в первом случае при делении на 2 получится 8 и 14), а во втором (4 и 7), то 51 разделить на 3 без столбика уже сложнее. Как происходит деление в столбик распишем на примере 51 разделить на 3.

Деление в столбик

• Как записывается делимое, делитель уже было сказано, визуально можно посмотреть выше на изображении. Делимое идет первым, потом ставится значок деления и над чертой пишут делитель.
• Теперь определяемся, сколько выделить цифр, чтобы начать подбирать множитель, который записывается под чертой в выделенный квадратик на изображении.
• Выделяем одну цифру 5-ку, она больше 3-ки, на черновике распишите примерно какой подобрать множитель, для того чтобы получить число ≤ 5, наглядно это выглядит так: 5 ≥ 3 · 1, число 1 и есть множитель. Его пишут под чертой делить в квадратике.
• Далее под пятеркой пишем произведение 3 · 1 = 3.
• Теперь вычитаем из 5 — 3 = 2. Разница, в нашем случае 2 должна быть < делителя, в нашем случае 3.
• Итак, остается разделить 21 на 3. Из таблицы умножения вы знаете, что: 21 : 3 = 7.
• Семерку пишут под чертой значка делить после единицы. Ответ получается 17.

Далее рассмотрим пример деления трехзначных чисел:

Давайте разделим трехзначное число 512 на 16. Деление будет происходить по той же схеме, что и двухзначного числа.

Пример деления трехзначного числа

• Запишите делимое, делитель, как на фото выше.
• Далее выделим число 51, и узнайте, сколько раз нужно взять число 16, чтобы получилось произведение меньше или равно 51. Итак, выше представлены расчеты: 16 · 3 = 48 < 51.
• Значит под чертой напишите 3, а под делимым 48. Теперь из 51 вычтите 48, получится 3, сносим следующую цифру 2.
• Подберите множитель к 16, чтобы произведение получилось равное или меньше 32. Итого: 16 · 2 = 32.
• Двойку запишите под черту знака деления, а результат 32 под делимым. Итого 32 — 32 = 0.
• Результат 32.

Рассмотрим деление многозначного числа:

Давайте найдем частное 998190 на 135, пример представлен на изображении ниже. Чтобы решить его, следует подставить нужные числа в пустых клетках.

Пример деления в столбик

• Итак, нужно найти первую цифру, на которое нужно умножить число 135, чтобы получить результат ≤ 998. Для этого понадобится знать отлично таблицу умножения и умение складывать цифры. 135 · 7 = 945.
• Число 945 пишите под делимым, вычтите из 998 — 945 = 53. Это число меньше 135, потому нужно снести еще одну цифру 1, получится 531.
• Высчитываем, какой множитель подойдет, к 135, чтобы получить число меньше, чем 534. Решение: 135 · 3 = 405.
• Вторая цифра под чертой знака деления 3, из 531 — 405 = 126.
• Сносим 9, выходит 1269, подбираем множитель к 135. Результат 135 · 9 = 1215.
• Третья цифра под чертой 9. Теперь: 1269 — 1215 = 54.
• Сносим 0, выходит 540, а 540 = 135 · 4, итого последняя цифра результата это 4.
• Результат 7394.

Деление чисел с нулями:

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

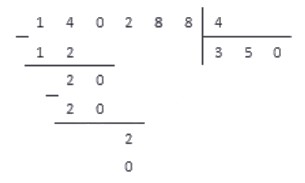
3. Выполняем операцию вычитания  и под чертой записываем результат.

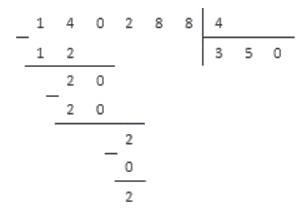
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

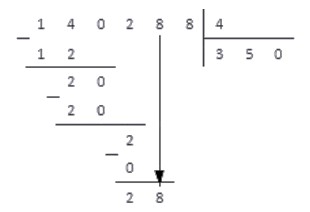
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

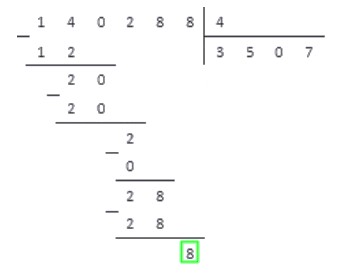
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

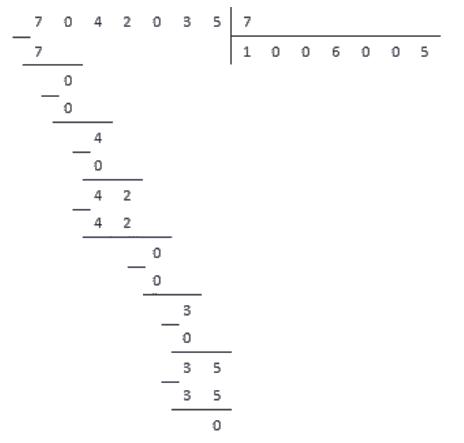
Ответ: 1006005

Разделение ячеек с помощью инструмента разделения текста Split text.

Теперь, когда вы знакомы со встроенными функциями, позвольте мне показать вам альтернативный способ разделения ячеек в Excel. Я имею в виду инструмент « , включенный в Ultimate Suite for Excel . Он может выполнять следующие операции:

• Разделить ячейку по символам
• Разделить ячейку по строке
• Разделить ячейку по маске (шаблону)

Например, разделение сведений об участнике из одной ячейки в несколько можно выполнить за 2 быстрых шага. Вот пример исходных данных:

1. Выделите ячейки, которые хотите разделить, и щелкните значок «Разделить текст (Split Text)» на вкладке «Ablebits Data» в разделе «Текст».

1. На панели «Разделить текст» настройте следующие параметры:
   • Выберите в качестве разделителей запятую и пробел.
   • Установите флажок Считать последовательные разделители одним.
   • В разделе «Выбор способа разделения ячеек» выберите «Разбить на столбцы (Split by columns)».
   • Нажмите кнопку «Разделить (Split)» .

Готово! Между исходными столбцами вставляются четыре новых столбца с разделенными данными, и вам нужно только дать этим столбцам соответствующие имена:

Совет: Инструмент «Разделить текст» предоставляет еще два параметра для разделения ячейки в Excel. Дополнительные сведения см. В  и « . 

Если вам интересно увидеть в действии инструменты «Разделить текст» и «Разделить имена» , можете загрузить 14-дневную пробную версию  Ultimate Suite for Excel. 

Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!

Деление в столбик

Такой тип примеров — один из любимых у детей. Он используется при работе с трех- и двузначными числами, которые сложно разделить в уме. Последовательность действий следующая:

Определить делимое и делитель: 648 — делимое, 36 — делитель. Записываем пример с помощью «уголка»: 

648|36; и начинаем подбирать значения, 36*2=72. 72 больше, чем 64, значит, этот вариант не подходит. 36*1=36, 36 меньше, чем 64 — это нужное нам число. Под 36 записываем 1. Продолжаем вести расчеты: 64-36=28, дописываем оставшееся число (648 — 64 мы уже использовали, осталось 8, которое мы и «сносим» к 28). Получается 288:36. Методом подбора определяем, что 36*10=360, 36*9=324, 36*8=288. Нужный результат получен, 288-288=0. Ответ:18. 

Перепроверяем себя, выполнив умножение в столбик или используя устный счет: 36*18, действительно получается 648 — ответ верный, все действия были выполнены правильно.

Деление с помощью таблицы умножения

Таблица умножения — удобный инструмент, который позволяет найти произведения однозначных натуральных чисел. Однако, ее можно использовать и для деления.

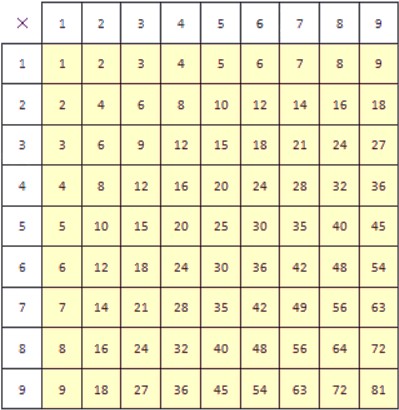
Таблица умножения позволяет находить не только результат произведения множителей, но и множитель по известному произведению и другому множителю. Как мы выяснили ранее, деление — это как раз и есть нахождение неизвестного множителя по известному произведению и еще одному множителю. 

С помощью таблицы умножения можно проводить деление любого числа на желтом фоне на любое однозначное натуральное число. Покажем, как это делать. Есть два способа, применение которых мы будем рассматривать на примерах.

Разделим 48 на 6.

Способ первый.

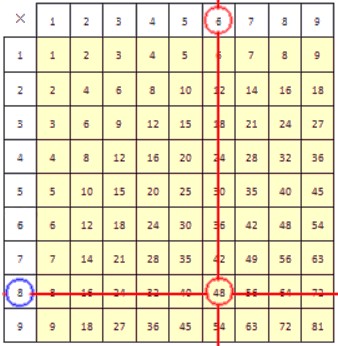
В столбце, верхняя ячейка которого содержит делитель 6, находим делимое 48. Результат деления при этом находится в крайней левой ячейке строки, содержащей делимое. Он обведен синей окружностью.

Способ второй. 

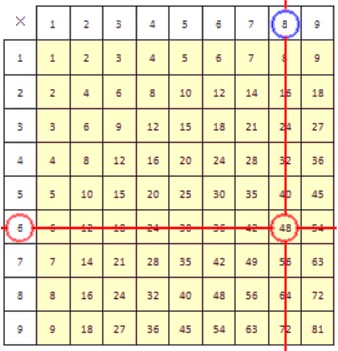
Сначала в строке с делителем 6 находим делимое 48. Результат деления при этом находится в крайней верхней ячейке столбца, содержащем делимое. Он обведен синей окружностью.

Итак, мы разделили 48 на 6 и получили 8. Результат был найден по таблице умножения двумя способами. Оба способа абсолютно идентичны.

Для закрепления рассмотрим еще один пример. Разделим 7 на 1. Приведем рисунки, иллюстрирующие процесс деления.

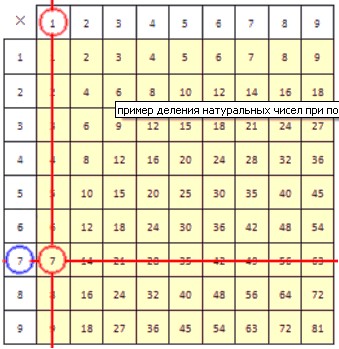
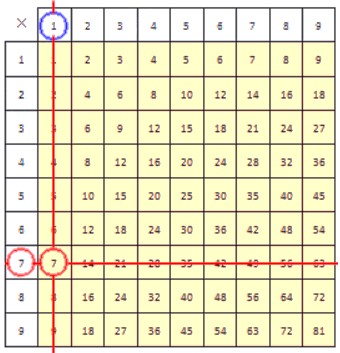
В результате деления числа 7  на  1, как вы уже догадались, получается число 7

В делении с помощью таблицы умножения очень важно знать эту таблицу наизусть, так как не всегда можно иметь ее под рукой

Настоятельно рекомендуем выучить таблицу умножения!

Основные приемы при делении

Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.

Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.

Чтобы разделить 27 на 3 мы пишем

Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое. Чтобы найти цифру частного, мы пробуем умножать делитель на разные числа или, как обыкновенно говорят, задаемся разными числами, и сравниваем произвдение делителя на частное с делимым.

Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.

Само вычисление выражают письменно:

Деление совершилось нацело.

Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.

Отыскивая целое частно, мы имеем при этом три случая:

1. Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:

   в остатке число 7 больше делителя 4. Это показывает, что частное 5 мало и его нужно увеличить.

2. Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.

3. Взяв для частного 6, мы ход вычисления выражаем письменно:

   словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:

Правило определения частного:

1. Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.

2. Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.

3. Если остаток меньше делителя, цифра частного верна.

Это правило показывает, что при делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя. Задаваться так, значит задаваться наибольшим целым числом.

В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и

27 = 4 × 6 + 3 = 24 + 3

Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.

Деление натурального числа на обыкновенную дробь

Правило деления аналогично правилу деления натурального числа на обыкновенную дробь: чтобы разделить натуральное число n на обыкновенную ab, необходимо произвести умножение числа n на обратное дроби ab.

Исходя из правила, имеем  nab=n·ba, а благодаря правилу умножения натурального числа на обыкновенную дробь, получим наше выражение в виде nab=n·ba. Необходимо рассмотреть данное деление на примере.

Пример 4

Делить 25 на 1528.

Решение

Нам необходимо переходить от деления к умножению. Запишем в виде выражения 251528=25·2815=25·2815. Сократим дробь и получим результат в виде дроби 4623.

Ответ: 251528=4623.

Правило деления целых отрицательных чисел, примеры

Для формулировки правила необходимо применить рассуждения. Если необходимо поделить целые отрицательные числа a на b, то искомое частное получится равным с. Форма записи: ab=c. После чего можно выяснить, чему равна абсолютная величина с.

Исходя из смысла деления равенство b·c=a справедливо. Значит, b·c=a. Благодаря свойствам модуля, можно записать равенство b·c=b·c, значит, и b·c=a. Отсюда получаем, что c=ab. Абсолютная величина частного от деления равняется частному от деления модулей делимого и делителя.

Для определения знака числа с необходимо выяснить, какие знаки находятся перед делимым и делителем.

Исходя из смысла деления целых чисел, равенство b·c=a справедливо. Правило умножения целых чисел говорит о том, что частное должно быть положительным. Иначе, b·c будет производиться по правилам целых отрицательных чисел. Частное с от деления целых отрицательных целых чисел является положительным числом.

Объединить в правило деления: чтобы разделить целое отрицательное число на отрицательное, необходимо разделить делимый на делитель по модулю. Эта запись будет выглядеть так ab=ab, при а и b равными отрицательным числам.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Рассмотрим несколько примеров деления отрицательных чисел.

Пример 3

Разделить -92 на -4.

Решение

Используя правила деления целых отрицательных чисел, получим, что следует делить по модулю. Получим, что -92-4=-92-4=924=23

Ответ: (−92)(−4)=23.

Пример 4

Вычислить -512 (-32).

Решение

Для решения необходимо разделить числа по модулю. Деление производится столбиком.

Ответ: (−512)(−32)=16.

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

Еще один пример деления

Деление натуральных чисел, оканчивающихся на нуль

При делении чисел, записи которых оканчиваются цифрой , полезно помнить свойство деления натурального числа на произведение двух чисел. При этом, делитель представляется в виде произведения двух множителей, после чего указанное свойство находит применение в совокупности с таблицей умножения.

Как всегда, поясним это на примерах.

Пример 7. Деление натуральных чисел, оканчивающихся на 0

Разделим 490 на 70.

Запишем 70 в виде:

70=7·10.

Используя свойство деления натурального числа на произведение, можно записать:

490÷70=490÷7·10=490÷10÷7.

Деление на 10 мы уже разобрали в предыдущем пункте.

490÷10÷7=49÷7=7

490÷70=7.

Для закрепления разберем еще один, более сложный пример.

Пример 8. Деление натуральных чисел, оканчивающихся на 0

Возьмем числа 54000 и 5400 и разделим их.

54000÷5400=?

Представим 5400 в виде 54·100 и запишем:

54000÷5400=54000÷54·100=54000÷100÷54=540÷54.

Теперь делимое 540 представляем в виде 54·10 и записываем:

540÷54=54·10÷54=54÷54·10=10

54000÷5400=10.

Подведем итог по изложенному в данном пункте.

Важно!

Если в записях делимого и делителя справа присутствуют нули, то нужно избавиться от одинакового количества нулей как в делимом, так и в делителе. После этого выполнить деление получившихся чисел.

Например, деление чисел 64000 и 8000 сведется к делению чисел 64 и 8.

История и философия ноля

На самом деле история с делением на ноль не давала покоя его изобретателям (а ноль изобрели в Индии). Но индийцы — философы привыкшие к абстрактным задачам. Что значит разделить на ничто? Для европейцев того времени такого вопроса вообще не существовало, так как ни о нуле ни об отрицательных числах (которые левее нуля на шкале) они знать не знали.

В Индии отнять от меньшего большее и получить отрицательное число не составляло проблем. Ведь что значит 3-5=-2 в обычной жизни? Это значит, что кто-то остался должен кому-то 2. Отрицательные числа назывались долгами.

Теперь давайте так же просто разберемся с вопросом деления на нуль. В далеком 598 году нашей эры (только вдумайтесь как давно, более 1400 лет назад!) в Индии родился математик Брахмагупта, который тоже задавался вопросом деления на ноль.

Он предположил, что если взять лимон и начать делить его на части, рано или поздно мы придем к тому, что дольки будут очень маленькими. В воображении мы можем дойти до того, что дольки станут равны нулю.

Итак, вопрос, если разделить лимон не на 2, 4 или 10 частей, а на стремящееся к бесконечности количество частей — какого размера получаться дольки? Получится бесконечное число «нулевых долек». Все довольно просто, нарежем лимон очень мелко, получим лужицу с бесконечным количеством частей — лимонный сок.

Достаточно задать самому себе вопрос:

х/ ∞=0 значит и х/0=∞

Что будет если поделить на ноль?

Но если взяться за математику, то получается как-то нелогично:

а*0=0? А если b*0=0? Значит: а*0=b*0

А отсюда: а=b

То есть любое число равно любому числу. Первая неправильность деления на ноль, идем дальше. В математике, деление считается обратным действием умножения. Это значит, что если мы делим 4 на 2, мы должны найти число, которое при умножении на 2 даст 4.

Делим 4 на ноль — нужно найти число, которое при умножении на ноль даст 4. То есть х*0=4? Но х*0=0! Опять незадача. Получается мы спрашиваем: «Сколько нолей нужно взять, чтобы получилось 4?» Бесконечность? Бесконечное количество нолей все равно даст в сумме ноль.

А деление 0 на 0 вообще дает неопределенность, ведь 0*х=0, где х вообще все что угодно. То есть — бесчисленное множество решений. Так что же получится в итоге?

Простое объяснение из жизни

Вот вам задачка из физики и реальной жизни. Допустим, мы хотим вычислит за сколько времени сможем пройти 10 километров. Значит Скорость * время = расстояние (S=Vt). Чтобы узнать время, расстояние делим на скорость (t=S/V). А что будет, если скорость у нас 0? t=10/0. Будет бесконечность!

Стоим на месте, скорость равна нулю, и с такой скоростью мы будем вечно добираться до отметки в 10 км. Значит время будет… t=∞. Вот и получилась у нас бесконечность!

И в этом примере делить на ноль можно, жизненный опыт позволяет. Жаль, что учителя в школе не могут объяснять такие вещи так же просто.

Еще одно объяснение

Давайте определимся, что такое деление? Например, 8/4 – означает вопрос «сколько четверок, может поместится в восьмерке?» Ответ: «две четверки», то есть математически 8/4=2.

А если задать себе вопрос 5/0=? Сколько нолей поместится внутри пятерки? Да сколько угодно. Бесконечное количество. Делим на ноль и получаем… снова бесконечность.

Но если вместо абстрактных цифр взять материальные вещи, например, яблоко. 6/3 — «если разложить 6 яблок по 3 в ящики, то сколько нужно ящиков?» Ответ: «2 ящика». Идем дальше 4/0 — «если разложить 4 яблока по ноль(!) штук в ящики, то сколько…» Получится, что ящики то не нужны, мы ничего никуда не кладем!

Совсем простое объяснение

Совсем просто, «на пальцах»

10/2=5 10/4=2,5 10/8=1,25 ….Чем больше число в знаменателе, тем меньше результат

10/2=5 10/1=10 10/0,5=20 ….Чем меньше число в знаменателе, тем больше результат, а если взять очень маленькое число? Например, 0,0000001 получится 1 00 000 000. И если пойти дальше в своих размышлениях и уменьшить знаменатель до нуля? В итоге получим что настолько огромное, что будет называться «бесконечность».

Какие растения можно размножать разделением?

Разделение — базовый вид вегетативного размножения комнатных растений, предусматривающий деление взрослого растения на несколько частей и высаживание каждой, как самостоятельного растения. Этот метод размножения используют как для получения потомства, так и для омоложения взрослых растений с наименьшими усилиями и травмами.

Он применяется для всех культур, кроме одноствольных и не дающих корневых отпрысков растений. Фактически, делить можно любые корневищные виды, растущие «в ширину» (группами или дернинами), и культуры, выпускающие дочерние растения у материнских клубней, луковиц и розеток. Одним словом, делят любое растение, не растущее в гордом одиночестве, у которого есть хотя бы несколько точек роста и способность образовывать поросль.

Этот метод размножения подходит большинству комнатных культур от луковичных до злаков, от почвопокровников до травянистых многолетников, независимо от их происхождения и степени капризности.

Это лучший метод размножения для многих комнатных любимцев: аспарагуса, сансевиерий, традесканций, солейролий, хавортий, зантедеский, аспидистры, спатифиллума, сенполий, кливии, стрептокарпуса, эхеверий, алоэ, агапантуса, плюща, папоротников, циперуса, примул, колокольчиков, маранты, орхидей, ананаса и других бромелиевых, калатеи, комнатных луковичных и пр.

Разделение не применяют для пальм, большинства каудексных, комнатных кустарников и древесных.

Способы деления

Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.

1. С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:

   4 + 4 + 4 = 12,

   следовательно, 4 содержится в 12 три раза.

2. С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:

   12 — 4 = 8
   8 — 4 = 4
   4 — 4 = 0

   Отсюда находим, что можно вычесть 4 из 12 ровно три раза.

   Деление есть сокращенное вычитание равных вычитаемых.

3. Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.

Способ 2: деление содержимого ячеек

Также в Excel можно делить данные, находящиеся в ячейках.

1. Выделяем в ячейку, в которую будет выводиться результат вычисления. Ставим в ней знак «=». Далее кликаем по месту, в котором расположено делимое. За этим её адрес появляется в строке формул после знака «равно». Далее с клавиатуры устанавливаем знак «/». Кликаем по ячейке, в которой размещен делитель. Если делителей несколько, так же как и в предыдущем способе, указываем их все, а перед их адресами ставим знак деления.

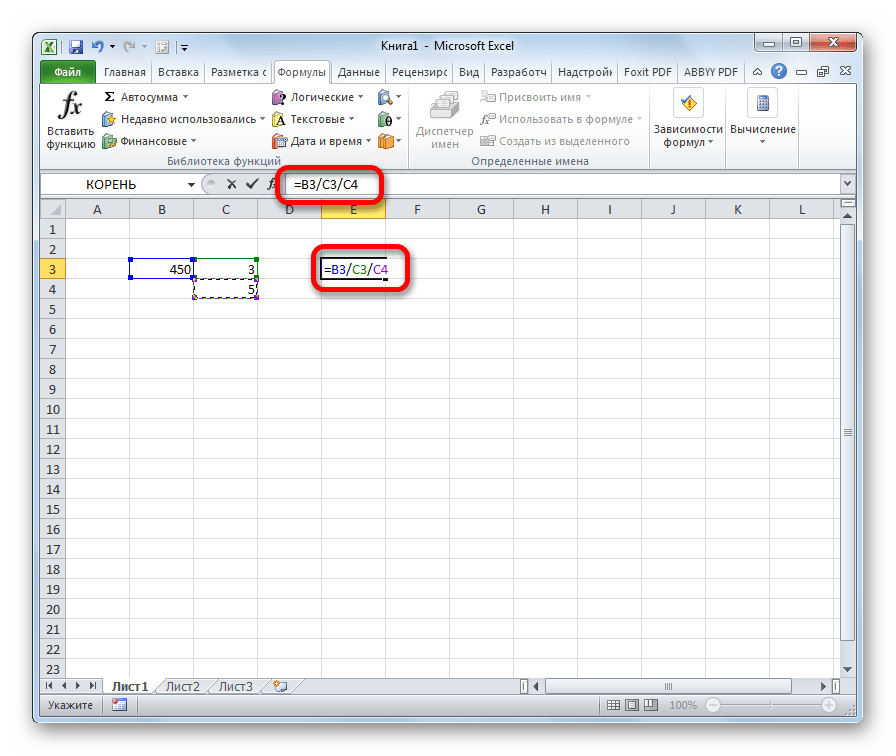
Для того, чтобы произвести действие (деление), кликаем по кнопке «Enter».

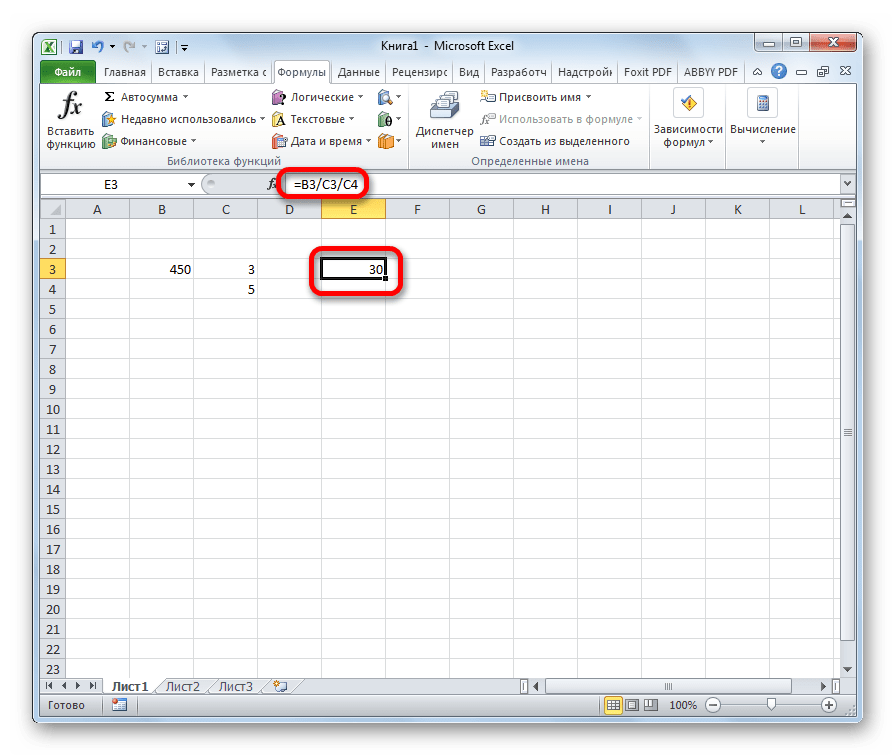
Можно также комбинировать, в качестве делимого или делителя используя одновременно и адреса ячеек и статические числа.

Заключение

Деление считается самой сложной операцией из четырех арифметических. И в виде готовой команды микроконтроллера оно встречается реже всего.
Но программная реализация оказалась вовсе не такой страшной, хотя и очень медленной по сравнению с аппаратно реализованными командами.
Для деления на известные на этапе написания программы константы лучше использовать комбинации сдвигов/вычитаний/сложений.
Увеличение
разрядности делимого не вызывает особых проблем и не ведет к резкому увеличению размера программ. Увеличение разрядности делителя гораздо
серьезнее, но непреодолимых трудностей тоже нет. Если же требуется делить числа с разрядностью многократно превышающей разрядность
микроконтроллера, то действительно имеет смысл задуматься о его замене на более подходящий.

Отмечу преимущество нашей реализации деления перед операцией деления в языках высокого уровня — мы сразу получаем и частное, и остаток. Да,
в stdlib есть функция div, которая тоже позволяет получить и частное, и остаток (структура div_t). Но, во первых, не
во всех компиляторах эта библиотека доступна. Во вторых, посмотрите на такую шедевральную, иначе и не скажешь реализацию
функции div в одном из компиляторов для 8-разрядных микроконтроллеров PIC

    div_t div(signed int numer, signed int denom) {
        div_t val;
        val.quot = numer / denom;
        val.rem = numer - (denom * val.quot);
        return (val);
    }

В 8 разрядных PIC команды деления нет, значит оно выполняется только программно. Как мы видели, при этом получается и частное,
и остаток. Но в этой реализации остаток предпочитают получать еще раз, причем через умножение! Замечу, что команда умножения есть
не во всех 8 разрядных PIC. Я не буду называть компилятор и его производителя. Но замечу, что это коммерческий компилятор, и
совсем не дешевый. Поэтому, знать описанные в этой статье алгоритмы деления может быть полезно даже в том случае, если Вы используете другие
контроллеры и всегда пишете программы только на языках высокого уровня.

Вы можете обсудить данную статью или задать вопросы автору на форуме